Topic 11: Zoeken en Sorteren¶

In wat voorafging hebben we reeds een aantal interessante algoritmen gezien voornamelijk om numerieke problemen op te lossen. T.t.z. we hebben Python gebruikt om wiskundige problemen uit te rekenen. In dit hoofdstuk gaan we verder met de studie van een aantal algoritmen die bij de kern van de computerwetenschappen horen. We spitsen onze aandacht toe op twee van de kerntaken die van computers zeer vaak verwacht worden: zoeken en sorteren.

“Het zoekprobleem” bestaat uit het vinden een gegeven data element in een grote hoop data. De toepassingen hiervan zijn haast niet te tellen. Denk maar aan een woordenboekapp waarin je verklaringen of vertalingen van een gegeven woord kan opzoeken, aan het elektronische telefoonboek dat in je GSM zit, aan Google die je snel de sites voor gevraagde sleutelwoorden kan leveren, enz. Omwille van de gigantische hoeveelheid toepassingen van “het zoekprobleem” is het mogelijk om hierover boeken vol te schrijven. In dit hoofdstuk beperken we ons tot de basis: we bestuderen de bekendste algoritmen om een element in een lijst te zoeken.

“Het sorteerprobleem” is al even alomtegenwoordig. Denk opnieuw aan het telefoonboek in je GSM dat alfabetisch gesorteerd is. Een ander voorbeeld is de “sort” menukeuze in het beroemde Excel rekenblad, waarmee je het rekenblad kan sorteren op een bepaalde kolom of rij. Ten slotte vermelden we nog “de flapjes” in iTunes waarmee je je playlists kan sorteren op titel, artiest, enz. Dit zijn allen voorbeelden van lijsten met gegevens erin die door de computer herschikt dienen te worden zodat de gegevens uiteindelijk in gesorteerde volgorde komen te staan.

Zoeken in Lijsten¶

Het eerste probleem waar we ons in dit hoofdstuk op toespitsen is het zoeken van de positie van een gegeven element in een gegeven lineaire datastructuur. Dit is wat achter de schermen gebeurt als je bijvoorbeeld een naam opzoekt in het telefoonboek van je GSM of als je een woord opzoekt in een elektronisch woordenboek. Concreet gaan we zoeken naar de index van een gegeven element in een Python lijst van lengte $n$. Maar een groot stuk van de bespreking en analyse geldt in het algemeen voor zoeken in een lineaire structuur. Bedoeling is dus om een Python functie find(lst,elm) te schrijven die het elementje elm opzoekt in de lijst lst. Op zich klinkt dit wat raar: waarom een element zoeken in een lijst als je dat element al vasthebt? Soms is het op zich belangrijk om te kunnen controleren of een gegeven element in een lange lijst voorkomt, i.e. heb ik een telefoonnummer voor Jan. Een andere nuance is dat find de index, i.e. de plaats van dat element gaat teruggeven. Je vindt dan in je telefoonbook naast de naam die je opzocht het telefoonnummer dat je zocht. Er moet ook een manier zijn om aan te geven dat het gezochte element niet in de lijst voorkomt. Onderstaande implementaties geven dan de lengte van de lijst terug. Herinner dat de grootst mogelijk index len(lst)-1 is, dus als je een te grote index terugkkrijgt weet je dat het element niet gevonden werd. Soms geven zoekalgoritmes bv. -1 of False terug om aan te geven dat het element niet gevonden werd. Op de plaats in je code waar je de find aanroept zal je dan moet controleren wat de terugkeerwaarde is en daarrond dan de juist beslissing nemen.

Lineair Zoeken¶

Het eerste algoritme waarmee we find kunnen realiseren heet lineair zoeken. Het is de meest naïeve oplossing van het probleem: we lopen m.b.v. een while lus gewoon de hele lijst van voor naar achter af op zoek naar het element.

De procedure initialiseert een tellertje idx op 0 en verhoogt dat (zie idx = idx+1) in elke slag van de iteratie. In de test van de while moeten we twee condities aftoetsen. Ten eerste dienen we ervoor te zorgen dat er gestopt wordt indien de hele lijst (onsuccesvol) werd doorlopen. Dit doen we door onze teller te vergelijken met de lengte van de lijst. Ten tweede dienen we na te kijken of we het gewenste elementje misschien gevonden hebben. In dat laatste geval wordt het zoekproces gestopt. De laatste lijn return idx geeft hetzij de correcte index weer, hetzij de lengte van de lijst om aan te geven dat het zoeken niet succesvol was.

def find(lst, elm):
    idx = 0
    while idx < len(lst) and lst[idx] != elm:
        idx = idx+1
    return idx

test = ["jan","ann","ils","jef","mia"]

find(test, "ils")

find(test, "theo")

We hebben in een aparte module Tracing een heleboel functies klaargezet die toelaten om de werking van de algoritmen in dit hoofdstuk op te volgen. We leggen deze niet uit omdat het gewoon een heleboel prutswerk is om in verschillende kleuren en geaccentueerd af te printen.

Voor de find wordt het element waarnaar gezocht wordt eerst in het geel afgeprint. Dan wordt voor elke slag van de iteratie de hele lijst waarin gezocht wordt uitgeprint. Daarbij worden verschillende kleuren gebruikt. Het element dat in deze iteratieslag vergeleken wordt, i.e. het element op positie idx wordt in het geel geaccentueerd. Alle elementen die in een vorige iteratieslag al werden bekeken staan geel gekleurd. Alle elementen die nog niet werden bekeken zijn blauw gekleurd. Tenslotte wordt de gevonden positie met een groen pijltje aangeduid of, indien het element niet in de lijst voorkomt wordt een rood kruis getoond.

De eerste trace toont hoe 3 wordt gevonden in de voorbeeldlijst [4,2,7,5,1,8,2,5,3,4,2,5] op de achtste positie. Er zijn daarvoor $9$ vergelijkingen gebeurd. De tweede trace toont dat er minder stappen nodig zijn als het gezochte element meer vooraan in de lijst staat. Het getal 2 wordt al gevonden na slechts 2 elementen bekeken te hebben. Het derde experimentje toont dat alle elementen van de lijst moeten afgelopen worden voor je kan concluderen dat een element niet aanwezig is.

from Tracing import *

test = [4,2,7,5,1,8,2,5,3,4,2,5]
show_find(test,3)


2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
                ^

test = [4,2,7,5,1,8,2,5,3,4,2,5]
show_find(test,2)


2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
  ^

test = [4,2,7,5,1,8,2,5,3,4,2,5]
show_find(test,6)


2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
2 7 5 1 8 2 5 3 4 2 5 
                        X

Wat is de snelheid van lineair zoeken? Het is duidelijk dat we in het beste geval het gezochte element meteen hebben gevonden, nml. in het geval het gezochte element helemaal vooraan in de lijst staat. De best-case is dus in $O(1)$. In het slechtste geval dienen we de hele lijst af te lopen en vinden we het elementje zelfs niet eens terug. De worst-case is dus in $O(n)$. Om te weten dat een element niet in een lijst zit zijn dus altijd $n$ vergelijkingen nodig. Om een element terug te vinden is een aantal stappen nodig ergens tussen 1 en n. Hoeveel juist hangt af van andere factoren zoals de verdeling van de waarden die in de lijst zitten.

Voor de volledigheid laten we nog een versie met for zien. Deze versie loopt alle mogelijke indices van de lijst af maar springt mogelijk uit de for-constructie m.b.v. de return. Dit eindigt de iteratie in geval van succes. De versie met for is iets minder stijlvol aangezien de bedoeling van een for-lus net is om alle indices af te lopen. Het manueel “uit de for-lus springen” maakt de code moeilijk om te lezen en te begrijpen. Bij het lezen van een while daarentegen weten we meteen dat het niet de bedoeling is van steeds de hele lijst af te lopen.

def find_bis(lst, elm):
    for idx in range(len(lst)):
        if lst[idx] == elm:
            return idx
    return len(lst)

test = ["jan", "ann","ils","jef", "mia"]

find_bis(test, "ils")

find_bis(test, "theo")

Binair Zoeken¶

Een radicaal andere manier om hetzelfde probleem op te lossen wordt binary search genoemd. Deze methode is heel nauw verwant met de bissectiemethode om nulpunten van functies te zoeken. We zullen de methode zowel recursief als iteratief uitwerken.

Binary search gaat ervan uit dat de elementen van de lijst gesorteerd zijn. Dit is een zeer belangrijke voorwaarde. Binary search werkt niet voor lijsten wier elementen niet gesorteerd zijn.

Binary search doet denken aan de manier waarop we een naam opzoeken in een telefoonboek. Men neemt het telefoonboek in de hand en opent het ongeveer in het midden. Afhankelijk van de pagina die we zien (bvb. met namen die beginnen met een K), beslissen we of de gezochte naam in het linker dan wel het rechterdeel van het boek moet zitten. Dit is mogelijk aangezien de gegevens gesorteerd zijn. Eens de keuze gemaakt, wordt dus de helft van de te doorzoeken data geëlimineerd! De gekozen helft wordt opnieuw in tweeën gedeeld en dit gaat door tot we op de juiste bladzijde terecht komen.

De recursieve implementatie van dit principe ziet er als volgt uit:

def bin_search(lst, elm):
    return bin_rec(lst,elm,0,len(lst)-1)

def bin_rec(lst, elm, left, right):
    if right < left:
        return len(lst)
    mid = (left + right)//2     #gehele deling om 'middelste' index te berekenen
    if lst[mid] == elm:
        return mid
    elif lst[mid] < elm:
        return bin_rec(lst, elm, mid+1, right)
    else:
        return bin_rec(lst, elm, left, mid-1)

test = ["ann","ils","jan", "jef", "mia"]

bin_search(test, "ils")

bin_search(test, "theo")

De functie bin_search neemt een lijst lst en het op te zoeken elementje elm. Ze geeft de index weer van het element in de lijst of de lengte van de lijst ingeval het element niet in de lijst voorkomt. bin_search roept meteen bin_rec. Dit is een hulpfunctie die zichzelf recursief aanroept en hierbij de twee variabelen left en right steeds dichter naar elkaar toe laat evolueren. In iedere slag van de recursie berekenen we de middelste index mid. Indien het gezochte element toevallig gevonden wordt op die index, zijn we klaar en geven we de index mid weer als eindresultaat. Anders vergelijken we het op te zoeken element met het element dat op die index zit en zoeken we op basis van de uitkomst van die vergelijking verder in de linker- of rechterhelft van de huidige opdeling.

Opnieuw kunnen we wat traces laten zien om de werking van het algoritme te bestuderen. De eerste trace laat zien dat het getal 7 gevonden wordt in de voorbeeldlijst [1,2,2,2,4,4,5,5,5,7,8,8] na slechts $4$ stappen. Voor elke recursieve oproep wordt de deellijst die aan de beurt is blauw afgeprint met het middelste element dat getest wordt in het geel geaccentueerd. De elementen die in de volgende stap geëllimineerd worden van de zoektocht kleuren grijs. Het aantal elementen dat getest werd is dus makkelijk te zien aan de gele accentkleur.

In het tweede experiment hebben we heel veel geluk. Het getal4 wordt al bij de eerste test gevonden omdat het net in het midden van de lijst staat. Het derde experiment toont dan weer het verloop van het algoritme als het element waar naar wordt gezocht niet in de lijst voorkomt. Ook hier is het aantal stappen beduidend lager dan bij lineair zoeken (4 i.p.v. 12 in ons voorbeeld).

test = [1,2,2,2,4,4,5,5,5,7,8,8]
show_bin_search(test, 7)


2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
                  ^

test = [1,2,2,2,4,4,5,5,5,7,8,8]
show_bin_search(test, 4)

4 
1 2 2 2 4 4 5 5 5 7 8 8 
          ^

test = [1,2,2,2,4,4,5,5,5,7,8,8]
show_bin_search(test, 3)


2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
2 2 2 4 4 5 5 5 7 8 8 
                        X

We kunnen hetzelfde algoritme ook iteratief schrijven. Er is naast het verschil van stijl en smaak een technisch verschil. Om recursie uit te voeren moet een computer onthouden naar welk punt hij na de recursieve oproep dient terug te springen. De recursieve versie zal hiervoor extra geheugen gebruiken en de iteratieve versie niet.

def bin_search_bis(lst, elm):
    left  = 0
    right = len(lst) - 1
    while left <= right:
        mid = (left + right) // 2 #gehele deling om 'middelste' index te berekenen
        if lst[mid] == elm:
            return mid
        if lst[mid] < elm:
            left=mid+1
        else:
            right=mid-1
    return len(lst)

test = ["ann","ils","jan", "jef", "mia"]

bin_search_bis(test, "ils")

bin_search_bis(test, "theo")

Dit keer zien we een functie met twee lokale variabelen left en right. In iedere slag van de iteratie berekenen we het midden en voeren we exact dezelfde tests uit als in de recursieve variante. Merk op dat de eindconditie in de recursieve versie precies de logische negatie is van de eindconditie in de while loop. Inderdaad, in de recursie is dat een voorwaarde om te stoppen terwijl het bij een while net een voorwaarde is om te blijven doorgaan. We zouden de conditie in de while kunnen veranderen in not right < left om dit nóg duidelijker te maken. Het resultaat zou natuurlijk (een klein beetje) trager zijn omdat Python dan in iedere slag van de iteratie ook nog de not moet uitvoeren.

Performantie

Wat kunnen we zeggen over de uitvoeringssnelheid van beide functies? Zowel in de iteratieve versie als in de recursieve versie moeten we het aantal iteratieslagen (resp. recursieve aanroepen) tellen. Als we geluk hebben, vinden we het gezochte element meteen de allereerste keer. De best-case is dus opnieuw in $O(1)$. Om de worst-case te bepalen, observeren we dat beide algoritmes vertrekken met twee variabelen left en right die respectievelijk de waardes 0 en len(lst)-1 krijgen en stoppen indien er geen verschil meer is tussen deze variabelen. In elke slag wordt ofwel left ofwel right “vervangen” door mid+1 of mid-1 zodat het verschil tussen left en right halveert in iedere slag. De vraag is dus hoeveel keer (laat ons zeggen, $k$) we $n=$ len(lst) kunnen halveren alvorens we $1$ uitkomen. Dus, voor welke $k$ is $\frac{n}{2^k}=1$? Dat is per definitie $k=log_2(n)$.

We kunnen dus stellen dat binair zoeken in $O(log_2(n))$ is. Merk op dat dit een dramatische(!) verbetering is t.o.v. lineair zoeken. Zelfs om een lijst van miljoenen elementen te doorzoeken heeft binair zoeken slechts enkele tientallen stappen nodig.

Enkele opmerkingen:

Eigenlijk is de basis van de logaritme niet relevant in een $O$ notatie. Vermits $log_2(x) = \frac{log(x)}{log(2)}$ en vermits $\frac{1}{log(2)}$ een constante is (dewelke geen rol spelen bij $O$), kunnen we stellen dat $O(log_2(n)) = O(log(n))$.
Alhoewel we het reeds vermeld hebben, is het nuttig te herhalen dat binair zoeken enkel toepasbaar is op gesorteerde data.

Experimentele Verificatie¶

De theoretische studie m.b.v. $O$ kan heel makkelijk experimenteel geverifieerd worden. We gaan meten hoe lang het duurt om in lijsten van oplopende lengtes te zoeken. We gebruiken in de experimenten lijsten met random getallen er in. We doen hiervoor beroep op de functie randint in de module random. Deze geeft een willekeurig geheel getal weer dat tussen beide parameters ligt. randint(1,100) geeft bijvoorbeeld een willekeurig getal tussen $1$ en $100$. Een lijst genereren van een gevraagde lengte met getallen die random gekozen zijn tussen grenzen 1 en n//2 kan makkelijk met een list comprehension zoals hieronder in de functie generate_lst gebeurt. De reden waarom we getallen genereren binnen grenzen die afhangen van de lengte van de lijst is om de kans dat een zelfde getal meer dan 1 keer voorkomt in alle lengtes van lijsten even groot te maken.

import random

def generate_lst(n):
    return [random.randint(1,n//2) for i in range(0,n)]

Het timen van de uitvoertijd van een functieoproep gebeurt zoals we al eerder deden met de time module.

import time

def time_find(lst,e):
    t1 = time.time()
    find(lst,e)
    t2 = time.time() 
    return (t2-t1)*1000

def time_bin_search(lst,e):
    t1 = time.time()
    bin_search(lst,e)
    t2 = time.time() 
    return (t2-t1)*1000

We maken een onderscheid tussen zoeken naar elementen die wel in de lijst voorkomen en zoeken naar elementen die niet in de lijst voorkomen. Het laatste is makkelijk, we zoeken bv. naar -1 terwijl we lijsten van positieve getallen gebruiken in onze tests. Voor het andere geval willen we een soort gemiddelde van zoeken naar elementen die eerder vooraan staan in de lijst en element die eerder achteraan staan in de lijst. We kunnen opnieuw de randint functie gebruiken om een random positie in de lijst die we onderzoeken te genereren. Als we dan gaan zoeken naar het element dat in de lijst op die positie staat zijn we dus zeker dat we zoeken naar een element dat voorkomt in de lijst. We gaan het tijdmeten telkens 50 keer herhalen en een gemiddelde gebruiken. We schrijven 4 functies om voor beide algoritmen 2 keer te timen, 1 keer voor het zoeken naar een element dat er zeker niet inzit, 1 keer voor het zoeken naar een element dat zeker wel in zit.

def time_find_nok(lst):
    return sum([time_find(lst,-1) for i in range(0,50)])/50
    
def time_find_ok(lst):
    return sum([time_find(lst,lst[random.randint(1,len(lst)-1)]) for i in range(0,50)])/50
    
def time_bin_search_nok(lst):
    return sum([time_bin_search(lst,-1) for i in range(0,50)])/50
    
def time_bin_search_ok(lst):
    return sum([time_bin_search(lst,lst[random.randint(1,len(lst)-1)]) for i in range(0,50)])/50   

We gaan teslotte met behulp van matplotlib 4 grafieken tekenen voor tijdsmetingen voor lijsten die variëren in lengte van $m$ tot $10$ keer $m$ met stappen van $m$. Dat kan door voor elke n in de range (m,m*10+1,m) een testlijst te genereren en daarvoor de tijdsmetingen uit te voeren met de 4 functies die we net schreven. De oproep plot_all_search_algo(1000) toont dus de tijdmetingen voor lijsten van lengte 1000 tot 10.000 met stappen van 1000.

import matplotlib.pyplot as plt

def plot_all_search_algo(m):
    x_values = list(range(m,10*m+1,m))
    y_values = [time_find_nok(generate_lst(m)) for m in range(m,10*m+1,m)]
    plt.plot(x_values,y_values, 'g^', label = "Find (False)")
    y_values = [time_find_ok(generate_lst(m)) for m in range(m,10*m+1,m)]
    plt.plot(x_values,y_values, 'ro', label = "Find (True)")
    y_values = [time_bin_search_nok(generate_lst(m)) for m in range(m,10*m+1,m)]
    plt.plot(x_values,y_values, 'bs', label = "Bin_search(False)")
    y_values = [time_bin_search_ok(generate_lst(m)) for m in range(m,10*m+1,m)]
    plt.plot(x_values,y_values, 'yd', label = "Bin_Search(True)")
    plt.ylabel('execution times for search algorithms')
    plt.legend()
    plt.show()        
    return "plot finished"

plot_all_search_algo(1000)

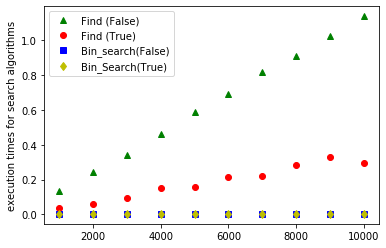
'plot finished'

De grafieken bevestigen de theoretische voorspellingen over het tijdsgebruik van de zoekalgoritmen. find is $O(n)$, beide grafieken zijn ongeveer rechten. Voor elementen die niet in de lijst zitten is de rechte stijler dan voor elementen die wel wel worden teruggevonden. Voor bin-search, theoretisch $O(log(n))$, zie je inderdaad dat de tijd nodig om een element te zoeken maar heel traag stijgt met de lengte van de lijsten. Je kan de codecel een paar keer uitproberen om pieken die het gevolg zijn van de andere dingen die je computer aan het doen is te vermijden of om met nog langere lijsten te testen. Let wel op, als je m heel groot kiest kan het wel een tijdje duren om alle tijdmetingen te doen.

Sorteren van Lijsten¶

Zoals reeds gezegd in de inleiding is sorteren een veelgebruikte functionaliteit voor computers. Maar hoe kan een computer een lijst van $n$ elementen in de juiste volgorde zetten? En hoe lang zal dat dan duren? In wat volgt onderzoeken we enkele sorteeralgoritmen en bestuderen we hun snelheid.

Insertion Sort¶

We beginnen met insertion sort. Dit is een zeer eenvoudig algoritme dat gelijkt op de manier waarop kaartstpelers hun kaarten in de juiste volgorde steken. Bij het delen van de kaarten zal degene die deelt de kaarten willekeurig op tafel leggen (met de rugzijde naar boven uiteraard, maar dat is hier niet relevant). Iedere kaarspeler zal dan beginnen met een lege hand en de gedeelde kaarten er met de andere hand één per één tussensteken in de juiste volgorde. Op ieder moment neemt de speler dus een volgende kaart — uit de ongesorteerde hoop — en steekt hij die (Eng: to insert) op de juiste plaats in de reeds-gesorteerde hand.

Indien we dit principe nu toepassen op ongesorteerde lijsten in Python, krijgen we het volgende algoritme:

def insertion_sort(lst):
    for idx in range(0, len(lst)):
        insert(lst,idx)
        
def insert(lst,idx):
    elm = lst[idx]
    while idx > 0 and lst[idx-1] > elm:
        lst[idx] = lst[idx-1]
        idx      = idx-1
    lst[idx] = elm

test = ["jan", "ann","ils","jef", "mia"]

insertion_sort(test)

test

['ann', 'ils', 'jan', 'jef', 'mia']

insertion_sort wandelt met een for ieder element in de lijst af, van links naar rechts. Ze roept voor iedere index idx de hulpfunctie insert op. Deze zal het idx’ste element van de lijst juist steken in de reeds gesorteerde elementen. Op ieder moment zal onze lijst bestaan uit twee (ongelijke) delen. Het linkerdeel is het reeds gesorteerde deel en het rechterdeel is het nog te sorteren deel. Telkens nemen we dus (met idx) het eerste elementje van het rechterdeel (wat steeds kleiner wordt) en steken we dat op de juiste plaats in het linkerdeel (wat steeds groter wordt). insert doet dat door in het linkerdeel van index idx te lopen naar 0 toe. Zolang we elementen zien die groter zijn dan het juist te steken element elm, schuiven we die 1 plaats naar rechts op. Anders steken we ons elementje op de zopas vrij gekomen plaats en zijn we klaar.

Om te volgen wat gebeurt tracen we hier eerst de werking van insert op een voorbeeldlijst waarvan de eerste 6 elementen al gesorteerd staan. De elementen die al ‘goed’ staan zijn groen gekleurd. We illustreren hoe het element op positie $6$ (in het voorbeeld het getal 3) naar de juiste positie verhuist door eerst alle elementen die groter zijn naar rechts op te schuiven. De gele kleur in de trace verduidelijkt welke elementen daarvoor bekeken en eventueel opgeschoven worden. De grijs weergegeven elementen spelen niet mee in deze insert stap.

test = [1,2,4,6,7,8,3,9,2,8,6,3]
show_insert(test,6)

2 4 6 7 8 3 9 2 8 6 3 
2 4 6 7 8   9 2 8 6 3 
2 4 6 7   8 9 2 8 6 3 
2 4 6   7 8 9 2 8 6 3 
2 4   6 7 8 9 2 8 6 3 
2   4 6 7 8 9 2 8 6 3 
2 3 4 6 7 8 9 2 8 6 3 

In de trace van insertion_sort zelf zie je dan dat startend van links telkens een extra element wordt ‘goed’ gezet. Je kan door de gele kleur ook vaststellen dat het aantal elementen dat daarvoor ‘bekeken’ wordt variabel is in elke iteratie slag maar kleiner dan of gelijk is aan het aantal elementen dat al gesorteerd staat in die iteratie slag.

test = [6,2,4,1,7,8,3,9,2,7,6,3]
show_insertion_sort(test)

2 4 1 7 8 3 9 2 7 6 3 
2 4 1 7 8 3 9 2 7 6 3 
2 4 1 7 8 3 9 2 7 6 3 
6 4 1 7 8 3 9 2 7 6 3 
4 6 1 7 8 3 9 2 7 6 3 
2 4 6 7 8 3 9 2 7 6 3 
2 4 6 7 8 3 9 2 7 6 3 
2 4 6 7 8 3 9 2 7 6 3 
2 3 4 6 7 8 9 2 7 6 3 
2 3 4 6 7 8 9 2 7 6 3 
2 2 3 4 6 7 8 9 7 6 3 
2 2 3 4 6 7 7 8 9 6 3 
2 2 3 4 6 6 7 7 8 9 3 
2 2 3 3 4 6 6 7 7 8 9 

Performantie

Wat is de snelheid van dit algoritme? De eerste keer moeten we een element tussenvoegen in een lijst van lengte $0$. De tweede keer moeten we een element tussenvoegen in een lijst van lengte $1$. De derde keer moeten we een element tussenvoegen in een lijst van lengte $2$. Enzoverder. De laatste keer moeten we een element toevoegen in een lijst van lengte $n-1$. In het allerslechtste geval is de data omgekeerd gesorteerd. In dat geval kost een element toevoegen in een lijst van lengte $i$ ons $O(i)$ computationele stappen. In totaal krijgen we dus $\displaystyle\sum_{i=1}^{n-1}{i} = \frac{1}{2}n(n-1) = O(n^{2})$ stappen. Insertion sort heeft een interessante best-case. Indien we de functie oproepen met een lijst die reeds gesorteerd is zal het tussenvoegen slechts 1 stapje vereisen (vergewis je hiervan met onderstaande trace). In dat geval is de totale hoeveelheid werk dus slechts $O(n)$. Inderdaad, de functie sort zal met de for alle elementen beschouwen en ze tussenvoegen (in 1 stap).

test = [1,2,3,4,5,6,7,8,9]
show_insertion_sort(test)

2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 

Selection Sort¶

Een tweede algoritme krijgen we door de omgekeerde redenering van insertion sort te maken. In de plaats van elementen goed te steken in het reeds gesorteerde deel, gaan we telkens het “volgende” element selecteren uit de nog te sorteren data. Vandaar de naam selection sort. Als we sorteren van klein naar groot zullen we dus telkens het kleinste element zoeken in het nog onbehandelde deel van de lijst en dat achteraan toevoegen aan het reeds gesorteerde deel van de lijst.

Onderstaande functies tonen een implementatie van selection sort in Python. De procedure selection_sort loopt alle indices idx af van links naar rechts. Opnieuw zal de lijst op ieder moment uit twee stukken bestaan. De data die links van idx zit is netjes gesorteerd en de data die rechts van idx zit is nog ongesorteerd. Op ieder moment zoeken we in de data rechts van idx de index van het kleinste element. Deze index noemen we sid (wat staat voor “smallest index”). Na afloop wisselen we het idx’ste element met het element dat op index sid zit en gaat for verder met de volgende idx. De rechtse hoop ongesorteerde data wordt dus steeds kleiner. Telkens opnieuw voegen we het kleinste element toe aan de gesorteerde rij die steeds langer wordt.

def selection_sort(lst):
    for idx in range(0, len(lst)):
        sid = select(lst,idx)
        lst[idx], lst[sid] = lst[sid], lst[idx] #verwissel
        
def select(lst,idx):
    sma = idx
    elm = lst[idx]
    while idx < len(lst):
        if lst[idx] < elm:
            sma = idx
            elm = lst[idx]
        idx = idx + 1
    return sma

select is de functie die in een lijst lst vanaf idx (tot het einde van de lijst) zoekt naar de index van het kleinste element. Op ieder moment is sma deze index en is elm dat element. Indien we bij het overlopen van de lijst een element lst[idx] tegenkomen dat nóg kleiner is, updaten we zowel sma als elm. We geven uiteindelijk de index sma van het kleinste element weer.

We kunnen opnieuw het algoritme testen door een lijstje te maken en de selection_sort functie erop los te laten. Het lijstje zal door de functie gemuteerd worden opdat alle elementen in de juiste volgorde komen te staan.

test = ["jan", "ann","ils","jef", "mia"]

selection_sort(test)

test

['ann', 'ils', 'jan', 'jef', 'mia']

Om te volgen wat gebeurt tracen we hier eerst de werking van select op een voorbeeldlijst waarvan de eerste 3 elementen al gesorteerd staan. We illustreren hoe vanaf het element op derde positie (in het voorbeeld het getal 6) naar het kleinste getal gezocht wordt in de rest van de lijst. De gele kleur in de trace verduidelijkt welke elementen daarvoor bekeken worden. De magenta kleur accentueert het element dat in elke iteratie als ‘kleinste tot nu toe’ is aangemerkt.

test = [1,2,2,6,9,4,2,6,4,7,8,3]
show_select(test,3)

2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 2 6 4 7 8 3 

In de trace van selection_sort zelf zie je dan dat startend van links telkens een extra element wordt toegevoegd aan het reeds gesorteerde voorste deel. Je kan door de gele kleur ook vaststellen dat om het kleinste element te vinden in de rest van de lijst alle elementen in de rest van de lijst moeten bekeken worden.

test = [4,2,8,6,9,4,2,6,1,7,8,3]
show_selection_sort(test)

2 8 6 9 4 2 6 1 7 8 3 
2 8 6 9 4 2 6 1 7 8 3 
2 8 6 9 4 2 6 4 7 8 3 
2 8 6 9 4 2 6 4 7 8 3 
2 2 6 9 4 8 6 4 7 8 3 
2 2 3 9 4 8 6 4 7 8 6 
2 2 3 4 9 8 6 4 7 8 6 
2 2 3 4 4 8 6 9 7 8 6 
2 2 3 4 4 6 8 9 7 8 6 
2 2 3 4 4 6 6 9 7 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 8 9 8 
2 2 3 4 4 6 6 7 8 8 9 
2 2 3 4 4 6 6 7 8 8 9 

Performantie

Wat is de snelheid van selection sort? Dit keer is er geen best-case die verschilt van de worst-case. We gaan in de for constructie van links naar rechts en roepen select aan. In select gaan we van idx helemaal tot het einde van de lijst (altijd!). De eerste keer zal select dus $n$ elementen doorlopen. De tweede keer zal dat maar $n-1$ elementen meer zijn. Daarna $n-2$. Enzoverder. De allerlaatste keer zal select nog een slechts $1$ element meer moeten doorlopen. In totaal krijgen we dus $\displaystyle\sum_{i=1}^{n}{i} = \frac{1}{2}n(n+1) = O(n^{2})$ stappen.

test = [1,2,3,4,5,6,7,8,9]
show_selection_sort(test)

2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 

Quicksort¶

Zowel insertion_sort als selection_sort algoritmen vertonen dus een $O(n^2)$ gedrag. Men zou kunnen denken dat dit het lot des levens is indien we een computer willen laten sorteren, maar dit is gelukkig niet het geval. We gaan nu over tot de bespreking van een algoritme dat veel sneller is. Het werd in de jaren $60$ uitgevonden door C.A.R. Hoare en staat bekend onder de naam quicksort. We zullen aantonen dat quicksort een performantie heeft die in $O(n.log(n))$ zit. Quicksort is niet het enige sorteeralgoritme dat in $O(n.log(n))$ zit maar wel het meest beroemde.

We zullen het quicksort algoritme uitleggen in 2 fasen. De eerste fase bestaat uit het begrijpen van het principe. We zullen dit illustreren aan de hand van de volgende (nogal inefficiënte) versie van quicksort. In de tweede fase zullen we hetzelfde algoritme dan herimplementeren met een scherper oog voor performantie en voor geheugengebruik.

def simple_quicksort(lst):
    if lst==[]:
        return []
    else:
        pivot   = lst[0]
        lesser  = simple_quicksort([x for x in lst[1:] if x < pivot])
        greater = simple_quicksort([x for x in lst[1:] if x >= pivot])
        return lesser + [pivot] + greater

Quicksort is een recursief algoritme dat een lijst opbreekt in deellijsten. Indien de invoerlijst leeg is, is het sorteren triviaal en is het resultaat de lege lijst. Indien de lijst niet leeg is, beschouwen we het element op de eerste plaats (t.t.z. lst[0]). We zullen dit element de pivot noemen. Dan lopen we door de lijst lst en plukken we er alle elementen uit die strikt kleiner zijn dan het pivot element en plukken we er alle elementen uit die groter zijn dan het pivot element. Dit resulteert in twee nieuwe lijsten die we allebei recursief sorteren. Het eindresultaat bestaat dan uit de gesorteerde lijst van elementen die kleiner zijn dan de pivot, gevolgd door de pivot, gevolgd door de gesorteerde lijst van elementen die groter zijn dan de pivot.

Bovenstaande code is op twee manieren nogal inefficiënt:

Om de twee deellijsten te bepalen wordt er twee keer door l[1:] gelopen.
Tijdens de recursie worden er in iedere recursieve oproep twee nieuwe lijsten gemaakt. Dit gebeurt door de twee list comprehensions in de code. Alle elementen worden door Python uit lst gekopieerd naar de nieuwe lijsten lesser en greater.

Een gevolg van dit laatste is dat wanneer we deze versie van het algoritme testen door een lijstje te maken en de simple_quicksort functie erop los te laten er een nieuwe lijst wordt teruggegeven die inderdaad dezelfde elementen als de originele lijst bevat in de juiste volgorde. Maar de originele lijst is niet veranderd.

test = ["jan", "ann","ils","jef", "mia"]

simple_quicksort(test)

['ann', 'ils', 'jan', 'jef', 'mia']

test

['jan', 'ann', 'ils', 'jef', 'mia']

De volgende code toont een “standaardversie” van quicksort die deze problemen niet heeft.

Er wordt slechts 1 keer door de lijst gelopen om meteen alle elementen kleiner dan de pivot te scheiden van de elementen die groter zijn dan de pivot.
Het geheel werkt in op de originele lijst door de deellijsten te bekijken als stukken van de originele lijst die afgebakend zijn m.b.v. een koppel indices die variëren doorheen de uitvoering van het algoritme.

def quicksort(lst):
    quick_rec(lst,0,len(lst)-1)
    
def quick_rec(lst,l,r):
    if l < r:
        m = partition(lst, l, r)
        quick_rec(lst, l, m-1)
        quick_rec(lst, m+1, r)
    
def partition(lst,l,r):
    pivot = lst[l]
    i = l+1
    j = r
    while i <= j:
        while i <= j and lst[i] < pivot:
            i = i + 1
        while i <= j and pivot <= lst[j]:
            j = j - 1
        if i < j:
            lst[i], lst[j] = lst[j], lst[i]
    lst[l], lst[j] = lst[j], pivot
    return j

Het basisprincipe achter dit algoritme is exact hetzelfde. De uitwerking is echter veel vernuftiger. In plaats van de lijst op ieder niveau van de recursie daadwerkelijk op te delen in $2$ verse lijsten en de gesorteerde versies van die lijsten dan opnieuw aan elkaar te plakken m.b.v. +, gaan we alle data laten zitten in de originele lijst maar dan wel op andere plaatsen. quicksort aanroepen op een testlijst heeft als effect dat de elementen in de lijst op volgorde komen te staan.

test = ["jan", "ann","ils","jef", "mia"]

quicksort(test)

test

['ann', 'ils', 'jan', 'jef', 'mia']

Het is de taak van de partition hulpfunctie om een stuk lijst tussen de grenzen l en r goed te zetten. Het eerste elementje (t.t.z. op lst[l]) wordt als pivot gekozen. Vanaf dan gaat partition de elementen zodanig herschikken dat alle elementen tussen l en r die kleiner zijn dan de pivot links van de pivot komen te staan, en zodanig dat alle elementen tussen l en r die groter dan of gelijk zijn aan de pivot rechts van de pivot komen te staan. De pivot zal dus het enige element zijn dat op zijn juiste plaats komt te staan. Die plaats wordt met return teruggegeven uit partition en wordt de m in de recursieve hoofdfunctie. Al wat deze dus nog moet doen is het algoritme recursief aanroepen voor beide helften, t.t.z. één keer tussen l en m-1 en één keer tussen m+1 en r.

Hoe gaat partition tewerk? De functie werkt met twee wijzertjes i en j. i vertrekt van links vlak na de pivot en werkt naar rechts toe. j vertrekt van het rechter einde en werkt naar links toe. i wordt naar rechts opgeschoven (doe i=i+1) zolang de elementen die we tegenkomen kleiner zijn dan de pivot. j wordt naar links opgeschoven (doe j=j-1)zolang de elementen die we tegenkomen groter dan of gelijk zijn aan de pivot. De extra testen in de binnenste while lussen zijn om niet ‘uit’ het deel van de lijst te vallen waar we op dit moment in geïnteresseerd zijn.

Op moment dat deze binnenste while lussen stoppen en i nog kleiner is dan j wisselen we de elementen op index i en j zodat het element kleiner dan de pivot links komt te staan en het element groter dan de pivot rechts komt te staan.

Opnieuw gaan we dan de buitenste while lus in om i en j verder naar elkaar toe te laten schuiven. Na verloop van tijd zullen de wijzertjes i en j mekaar raken of voorbij lopen. Op dat moment is j de plaats waar de pivot terecht moet komen. We wisselen dan de pivot met het elementje lst[j] zodat de pivot op zijn plaatst staat.

We illustreren hieronder de werking van partition door een voorbeeldlijst te laten zien die zal opgedeeld worden door haar eerste element als pivot te gebruiken. We accentueren voor elke iteratieslag van de buitenste while de indexen i en j op hun startpositie in magenta. In binnenste while lussen schuift i naar rechts en j naar links tot een element wordt gevonden dat groter, respectievelijk kleiner is dan de pivot. We kleuren de elementen die daarbij bekeken worden in magenta. Dan volgt een verwisseling. Na de verwisseling kleuren de reeds bekeken elementen geel. Dat gaat zo door tot i en j elkaar voorbij lopen en dan wordt de pivot naar de juiste positie verplaatst. Hij wordt dat groen geaccentueerd. Alle elementen links van de pivot (het getal 7 op positie $10$) zijn nu kleiner dan de pivot, al de getallen rechts er van zijn groter. De gele kleur duidt aan dat ze bekeken werden.

test = [7,3,8,2,4,1,8,9,4,6,2,6,3,6,9,8]
show_partition(test,0,len(test)-1)

3 8 2 4 1 8 9 4 6 2 6 3 6 9 8 

3 8 2 4 1 8 9 4 6 2 6 3 6 9 8 
3 > 2 4 1 8 9 4 6 2 6 3 < 9 8 

3 6 2 4 1 8 9 4 6 2 6 3 8 9 8 
3 6 2 4 1 > 9 4 6 2 6 < 8 9 8 

3 6 2 4 1 3 9 4 6 2 6 8 8 9 8 
3 6 2 4 1 3 > 4 6 2 < 8 8 9 8 

3 6 2 4 1 3 6 4 6 2 9 8 8 9 8 
3 6 2 4 1 3 6 4 6 < > 8 8 9 8 

3 6 2 4 1 3 6 4 6 7 9 8 8 9 8 

We illustreren nu quicksort zelf. Het is een boomrecursief algoritme. Om de opeenvolgende aanroepen op te volgen wordt iedere keer het stuk lijst tussen de posities l en r dat onder handen genomen wordt in het blauw getoond. De pivot wordt in het geel geaccentueerd. De rest van de lijst wordt in die aanroep niet bekeken en wordt daarom in het grijs getoond. We accentueren ook de pivot van de vorige recursiestap in het groen. Bij het terugkeren uit de recursie kleurt de lijst stukje bij stukje groen omdat die elementen dan ‘goed’ staan.

test = [7,2,4,8,6,9,4,2,6,1,8,3]
show_quicksort(test)

2 4 8 6 9 4 2 6 1 8 3 
2 4 3 6 1 4 2 7 9 8 8 
2 4 3 2 1 6 6 7 9 8 8 
2 1 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 9 8 8 
2 2 3 4 4 6 6 7 8 8 9 
2 2 3 4 4 6 6 7 8 8 9 
2 2 3 4 4 6 6 7 8 8 9 
2 2 3 4 4 6 6 7 8 8 9 

Performantie

Om de snelheid van quicksort te bepalen zullen we het totaal aantal stappen tellen dat het algoritme dient uit te voeren. Al wat we dienen te doen is de som te nemen van het totaal aantal stappen die ooit door het algoritme zullen uitgevoerd worden. Noteer $W_{i}(n)$ als de totale hoeveel vergelijkingen en verwisselingen (t.t.z. de hoeveelheid werk) die zullen uitgevoerd worden in het $i^{de}$ niveau van de recursie. We hebben duidelijk $W_{0}(n) = n$ vermits het nulde niveau de hele lijst moet doorlopen. $W_{1}(n) = n-1$ omdat het nulde niveau de pivot goed heeft gestoken zodat beide recursieve oproepen in totaal alle elementen zullen beschouwen behalve de reeds goedgestoken pivot. Op dit ogenblik dienen we een onderscheid te maken tussen de best-case en de worst-case.

Best-case Analyse:

In het beste geval hebben we steeds zeer veel geluk en zal de pivot zodanig zijn dat er precies evenveel elementen kleiner dan de pivot zijn, als er elementen zijn die groter dan de pivot zijn. In dat geval wordt de lijst tussen l en r op ieder recursieniveau perfect in tweeën verdeeld. In beide recursieve oproepen tesamen zullen er opnieuw twee pivot’s worden goedgestoken. Bijgevolg is $W_{2}(n) = n-3$. In het algemeen krijgen we op het $i^{de}$ niveau van de recursie een hoeveelheid werk die correspondeert met $W_{i}(n) = n- (2^{i}-1)$. Om te weten hoeveel recursieniveaus er zoal zijn, dienen we te weten hoe dikwijls we een lijst van lengte $n$ door $2$ kunnen delen. Het antwoord hierop is natuurlijk $log_{2}(n)$. In het beste geval moeten we dus al het werk bij elkaar tellen voor $log_{2}(n)$ niveaus in de recursie. M.a.w. $\displaystyle\sum_{i=0}^{log_{2}(n)}{W_{i}(n)}$. Bijgevolg:

\[\begin{split}\begin{aligned} \displaystyle\sum_{i=0}^{log_{2}(n)}{W_{i}(n)} & = & \displaystyle\sum_{i=0}^{log_{2}(n)}{n- (2^{i}-1)} \nonumber \\ & = & \displaystyle\sum_{i=0}^{log_{2}(n)}{n} - \displaystyle\sum_{i=0}^{log_{2}(n)}{2^{i}} + \displaystyle\sum_{i=0}^{log_{2}(n)}{1} \nonumber \\ & = & n.log_{2}(n) - \left( \frac{2^{log_{2}(n)+1}-1}{2-1} \right) + log_{2}(n) \nonumber \\ & = & n.log_{2}(n) - \left( 2.2^{log_{2}(n)}-1 \right) + log_{2}(n) \nonumber \\ & = & n.log_{2}(n) - (2.n -1 ) + log_{2}(n) \nonumber \\ & = & O(n.log(n)) \nonumber \end{aligned}\end{split}\]

Worst-case Analyse:

Maar we kunnen echter ook heel veel tegenslag hebben. Stel dat we quicksort toepassen op een lijst die reeds gesorteerd is. In dat geval zal de pivot steeds het kleinste element zijn van alle elementen tussen l en r. Er zullen dus geen elementen links van de pivot komen en alle elementen zullen rechts van de pivot komen te staan. In ieder niveau van de recursie wordt er dus slechts $1$ stapje minder werk gedaan dan in het vorige niveau, of nog $W_{i}(n) = n-i$. De linkse recursieve oproep zal dus geen werk verrichten en meteen terugkeren. De rechtse recursieve oproep moet al het werk doen, behalve het ene stapje van het vorige niveau. We krijgen dus in totaal $n$ recursieve oproepen. Alles bij elkaar tellen geeft dit keer dus $\displaystyle\sum_{i=0}^{n}{W_{i}(n)}$. Indien we dit opnieuw uitrekenen krijgen we een uitkomst in $O(n^{2})$

Onderstaande trace illustreert dit. Er zijn 9 aanroepen nodig om een reeds gesorteerde lijst van 9 elementen te sorteren.

test = [1,2,3,4,5,6,7,8,9]
show_quicksort(test)

2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 

Een gelijkaardig scenario doet zich voor bij een invoerlijst die omgekeerd gesorteerd is. Er zullen nu geen elementen rechts van de pivot komen en alle elementen zullen links van de pivot komen te staan. In ieder niveau van de recursie wordt er dus slechts $1$ stapje minder werk gedaan dan in het vorige niveau. De rechtse recursieve oproep zal dus geen werk verrichten en meteen terugkeren. De linkse recursieve oproep moet al het werk doen, behalve het ene stapje van het vorige niveau. We krijgen dus in totaal $n$ recursieve oproepen zoals de trace hieronder illustreert.

test = [9,8,7,6,5,4,3,2,1]
show_quicksort(test)

8 7 6 5 4 3 2 1 
8 7 6 5 4 3 2 9 
8 7 6 5 4 3 2 9 
2 7 6 5 4 3 8 9 
2 7 6 5 4 3 8 9 
2 3 6 5 4 7 8 9 
2 3 6 5 4 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 
2 3 4 5 6 7 8 9 

Performantieverbetering

Quicksort is een zeer goed sorteeralgoritme. Men kan met voldoende harde wiskunde aantonen dat het gemiddelde geval toch in $O(n.log(n))$ zit. Het bovenstaande worst-case geval is dus een pathologisch geval. Maar het is helaas een pathologisch geval dat zich in de praktijk redelijk dikwijls voordoet. Indien we bvb. in iTunes $2$ keer op hetzelfde flapje clicken, is het de bedoeling dat de reeds gesorteerde playlist in de omgekeerde volgorde gesorteerd dient te worden. In dat geval zou quicksort dus zeer slecht scoren. Men zegt dat quicksort ontaardt (of ook wel: degenereert). Er zijn hier verschillende mouwen aan te passen die buiten het bestek van deze cursus vallen. Eén van de eenvoudigste bestaat erin van helemaal in het begin van iedere partition het eerste element (onze oude pivot dus) te verwisselen met een willekeurig element dat tussen l en r zit. Deze randomized quicksort blijkt in de praktijk vrij goed te werken. Een variant die geen random functie nodig heeft is om als pivot de mediaan te kiezen van het eerste, het laatste en het middelste element van de lijst.

Experimentele Verificatie¶

Het is leerrijk om de theoretische studie m.b.v. $O$ te vergelijken met de echte data die uit een profile komt. We gebruiken in de experimenten lijsten met random getallen er in. We doen hiervoor beroep op de functie randint in de module random. Deze geeft een willekeurig getal weer dat tussen beide parameters ligt. randint(1,100) geeft bijvoorbeeld een willekeurig getal tussen $1$ en $100$.

Een lijst genereren van een gevraagde lengte met getallen die random gekozen zijn tussen grenzen 1 en n//2 kan makkelijk met een list comprehension zoals hieronder in de functie generate_lst gebeurt. De reden waarom we getallen genereren binnen grenzen die afhangen van de lengte van de lijst is om de kans dat een zelfde getal meer dan 1 keer voorkomt in alle lengtes van lijsten even groot te maken.

import random

def generate_lst(n):
    return [random.randint(1,n//2) for i in range(0,n)]

Het timen van de functieaanroep gebeurt zoals we al eerder deden met de time module.

import time

def time_insertion_sort(lst):
    t1 = time.time()
    insertion_sort(lst)
    t2 = time.time() 
    return (t2-t1)

def time_selection_sort(lst):
    t1 = time.time()
    selection_sort(lst)
    t2 = time.time() 
    return (t2-t1)

def time_quicksort(lst):
    t1 = time.time()
    quicksort(lst)
    t2 = time.time() 
    return (t2-t1)

Met behulp van Matplotlib gaan we nu 3 grafieken uitzetten door de tijdmetingen te doen voor de 3 algoritmen voor random gegenereerde lijsten met lengtes oplopend van $m$ tot $10$ keer $m$ met stappen van $m$. Dat kan door voor alle n in de range(m,m*10+1,m) een lijst te genereren met lengte n, het sorteren van de lijst te timen, en de meetwaarden uit te zetten. Let op, voor grote $m$ kan dit wel eventjes duren.

import matplotlib.pyplot as plt

def plot_all_sort_algo(m):
    x_values = list(range(m,m*10+1,m))
    y_values = [time_insertion_sort(generate_lst(n)) for n in range(m,m*10+1,m)]
    plt.plot(x_values,y_values, 'g^', label = "InsSort")
    y_values = [time_selection_sort(generate_lst(n)) for n in range(m,m*10+1,m)]
    plt.plot(x_values,y_values, 'ro', label = "SelSort")
    y_values = [time_quicksort(generate_lst(n)) for n in range(m,m*10+1,m)]
    plt.plot(x_values,y_values, 'yd', label = "Quicksort")
    plt.ylabel('execution times for 3 sorting algorithms')
    plt.legend()
    plt.show()        
    return "plot finished"

Het resultaat voor lijsten met lengtes van 1000,2000,…, tot 10.000 wordt getoond in onderstaande figuur. De theoretische voorspellingen (t.t.z. $O(n.log(n))$ en $O(n^2)$) worden netjes experimenteel bevestigd. De grafieken voor insertion sort en selection sort zijn parabolen. De grafiek voor quicksort is veel platter. Een lijst sorteren met 10.000 elementen met een basis sorteeralgoritme neemt al enige tijd. De tijd die quicksort nodig heeft is significant kleiner. In twee kleine experimenten onder de grafiek zie je dat quicksort een lijst van 1 miljoen elementen kan sorteren binnen de tijd die insertion-sort nodig heeft om tienduizend elementen te sorteren.

plot_all_sort_algo(1000)

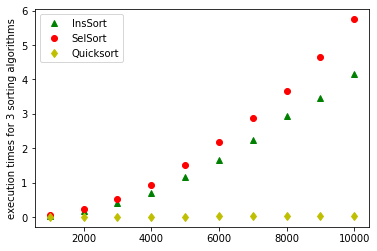
'plot finished'

test = generate_lst(10000)
time_insertion_sort(test)       

4.237020969390869

test = generate_lst(1000000)
time_quicksort(test)       

3.7103018760681152

De theoretische O(n.log(n)) ondergrens¶

Zijn er grenzen aan de snelheid van algoritmen? Voor sommige problemen is dit een onopgeloste vraag. Voor sorteren is het antwoord bekend: nooit zal een algemeen sorteeralgoritme gevonden worden dat de $O(n.log(n))$ performantie verslaat. Met een “algemeen” algoritme wordt bedoeld een algoritme dat enkel gebruik maakt van “vergelijken van elementen” en “verplaatsen van elementen”. Er bestaan algoritmen die toch sneller kunnen, maar deze zijn dan enkel toepasbaar op specifieke soorten gegevens. Zo is bvb. counting sort in $O(n+k)$ enkel toepasbaar op positieve gehele getallen waarbij de tweede factor k relateert aan de grootte van de getallen die worden gesorteerd.

Als afsluiting van deze topic leveren we het wiskundig bewijs voor onderstaande stelling over algemene sorteeralgoritmen.

Stelling:

Het is onmogelijk een algemeen sorteeralgoritme te schrijven dat sneller gaat dan $n.log(n)$.

Bewijs:

Beschouw een rij $e_{0}$, $e_{1}$, $e_{2}$, …, $e_{l-1}$ van $n$ data elementen die gesorteerd dienen te worden. Een algemeen algoritme gebaseerd op vergelijken van elementen zal dus heel de tijd bezig zijn met het vergelijken van 2 elementen gevolgd door eventueel verplaatsen van die 2 elementen. Uiteindelijk betekent sorteren dat we de elementen op een bepaalde manier herordenen, d.w.z. permuteren. De lijst na het sorteren is immers een permutatie van de lijst vóór het sorteren. En uit de wiskunde weten we dat er $n!$ mogelijke permutaties zijn voor een lijst van lengte $n$.

We kunnen alle mogelijke uitvoeringen van een sorteeralgoritme tekenen in de vorm van een beslissingsboom. Als illustratie genereert de functie show_decision_tree die we knutselden in de module Pretty_print de figuur hieronder. Deze boom toont alle mogelijke gevallen voor $n=3$ elementen. Iedere knoop in die boom bestaat uit de vergelijking van twee elementen. Afhankelijk van het resultaat van die vergelijking gaat het algoritme verder met het vergelijken van twee andere elementen. Afhankelijk van de initiële volgorde van de elementen zal de uitvoering van het algoritme corresponderen met één pad (van de top naar een blad) in die boom.

from Pretty_print import *
print_decision_tree()

                                       e₁<e₂
                      ___________________|_________ 
                     |                             |
                   e₀<e₁                         e₀<e₁
                 ____|_________                ____|_________ 
                |              |              |              |
              e₀e₁e₂         e₀<e₂          e₀e₂e₁         e₀<e₂
                           ____|____                     ____|____ 
                          |         |                   |         |
                        e₁e₀e₂    e₁e₂e₀              e₂e₀e₁    e₂e₁e₀

We weten dat die boom $n!$ mogelijke bladeren heeft omdat er $n!$ permutaties bestaan. Dus hebben we zeker meer dan $n!$ mogelijke knopen en dus is de hoogte van de boom $h$ zeker hoger dan $log(n!)$. Vermits nu $log(n!) > n.log(n)$ voor grote $n$ kunnen we concluderen dat $h > n.log(n)$. Met de wetenschap dat $h$ het aantal vergelijkingen is (d.w.z. de hoogte van de beslissingsboom), krijgen we dus dat er minstens minstens $n.log(n)$ stappen ondernomen moeten worden.

We moeten dus nog aantonen dat $log(n!) > n.log(n)$ voor alle $n$ vanaf een bepaalde $n_0$. Hier is een eenvoudig bewijs:

\[\begin{split}\begin{aligned} log(n!) & = & \displaystyle\sum_{i=1}^{n}{log(i)} \\ & > & \displaystyle\sum_{i=\lceil(\frac{n+1}{2})\rceil}^{n}{log(i)} \\ & > & \displaystyle\sum_{i=\lceil(\frac{n+1}{2})\rceil}^{n}{log(\frac{n}{2})} \\ & > & \frac{n}{2}.log(\frac{n}{2}) \\ & = & \frac{n}{2}.(log(n) - 1) \\ & = & \frac{n.log(n)}{2} - \frac{n}{2} \\ & > & \frac{n.log(n)}{2} - \frac{n.log(n)}{6} \textrm{~~indien $n>8$}\\ & = & \frac{1}{3}n.log(n) \\\end{aligned}\end{split}\]

Dus is $log(n!) > \frac{1}{3}.n.log(n)$ voor alle $n > n_0=8$.

Conclusie¶

In dit hoofdstuk hebben we twee van de belangrijkste problemen onderzocht waarvoor computers gebruikt worden: het zoeken van gegevens in een (grote) hoop gegevens en het sorteren van gegevens in de juiste volgorde. We hebben voor deze twee problemen ook de theoretische $O$ besproken.

Inleiding tot de Computerwetenschappen

Topic 11: Zoeken en Sorteren¶

Zoeken in Lijsten¶

Lineair Zoeken¶

Binair Zoeken¶

Experimentele Verificatie¶

Sorteren van Lijsten¶

Insertion Sort¶

Selection Sort¶

Quicksort¶

Experimentele Verificatie¶

De theoretische O(n.log(n)) ondergrens¶

Conclusie¶