TOPIC 5: Lijsten¶
We hebben in de vorige topics geprobeerd een gezond evenwicht te houden tussen het introduceren van Python als taal en het gebruik van de taal om concepten uit de computerwetenschappen te bestuderen. Zo hebben we na het leren oproepen van functies gezien hoe we plots kunnen maken en hebben we na het leren schrijven van functies het fenomeen recursie bestudeerd in het vorige hoofdstuk.
In dit hoofdstuk gaan we weer even verder met het uitbreiden van onze Python kennis. We introduceren lijsten die samen met tupels een nieuwe techniek vormen om samengestelde data te maken. We leggen het verschil uit tussen lijsten en tupels en we bestuderen de operatoren en functies die op lijsten toepasbaar zijn. Een zeer krachtig instrument om vrij ingewikkelde lijsten te maken zijn de list comprehensions. Ook deze worden uitvoerig behandeld.
Een tweede belangrijke toevoeging aan onze Python kennis die in dit
hoofdstuk zal worden geïntroduceerd is de iteratie m.b.v. de for
constructie. We hebben in het hoofdstuk over recursie al gezien dat we
recursieve functies kunnen gebruiken indien we Python een groep
statements steeds opnieuw willen laten herhalen (t.t.z. “itereren”). Met
de for constructie levert Python hiervoor echter nog extra
ondersteuning. Vooral voor het “aflopen” van lijsten, tupels en strings
is deze constructie bijzonder elegant.
We eindigen dit topic met twee grotere gevalstudies die de kracht van iteratie over lijsten laten zien. We zullen twee computersimulaties bouwen die beide een biologisch proces nabootsen. Herinner uit topic 1 dat het simuleren van de werkelijkheid steeds belangrijker wordt bij onderzoek in de (natuur)wetenschappen. We laten op het einde van dit hoofdstuk dan ook twee simulaties zien die we vrij eenvoudig kunnen programmeren met de Python kennis die we totnogtoe hebben opgebouwd. We simuleren een eenvoudige vorm van eiwitexpressie in de biochemie en de groei van populaties (bvb. vissen in een vijver) in de biologie. Beide simulaties zullen geprogrammeerd worden als een iteratie die een lijst van waarden opbouwt.
Een Nieuw Type: Lijsten¶
We beginnen met het introduceren van een nieuw type: lijsten van Python
waarden. Lijsten zijn net als tupels een manier om data samen te lijmen
tot wat men doorgaans een datastructuur noemt. Daar waar tupels
opgeschreven worden door hun componenten tussen ronde haakjes op te
sommen, worden lijsten genoteerd door hun componenten op te sommen
tussen vierkante haakjes. Net zoals bij tupels dienen de componenten
gescheiden te worden door komma’s. Hieronder zien we hoe een variabele
whales gedefinieerd wordt die een lijst bevat met getallen (in dit
geval: het aantal waargenomen walvissen voor een zekere kustlijn
gedurende \(2\) weken):
whales = [5, 4, 7, 3, 2, 3, 2, 6, 4, 2, 1, 7, 1, 3]
whales
[5, 4, 7, 3, 2, 3, 2, 6, 4, 2, 1, 7, 1, 3]
whales[0]
5
whales[6]
2
whales[-3]
7
De drie laatste experimentjes laten zien dat we lijsten — net als tupels — kunnen indexeren door de gewenste index tussen vierkante haken te zetten. Negatieve indices beginnen achteraan in de lijst. Uiteraard dienen deze indices te voldoen aan de grenzen van de lijst in kwestie. Hieronder zien we wat er gebeurt indien we de lijst indexeren op de (onbestaande) positie \(100\). Python klaagt dat de gegeven index buiten het bereik (Eng.: range) van de lijst valt.
whales[100]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
<ipython-input-6-894c5783e065> in <module>
----> 1 whales[100]
IndexError: list index out of range
Een zeer speciale lijst is de lege lijst. Deze noteren we met []. De
lege lijst is min of meer te vergelijken met de lege verzameling in de
wiskunde. Hij bevat geen enkel element en kan dus niet geïndexeerd
worden zoals wordt aangetoond in volgend experiment. Zelfs het indexeren op positie 0 levert al een foutmelding op!
fish = []
fish
[]
fish[0]
---------------------------------------------------------------------------
IndexError Traceback (most recent call last)
<ipython-input-9-fe936bed3b30> in <module>
----> 1 fish[0]
IndexError: list index out of range
Nesten van Lijsten¶
Net zoals we tupels van tupels kunnen maken
en we if-testen in if-testen kunnen zetten, kunnen
we ook lijsten in lijsten stoppen. We noemen dit fenomeen nesten van
lijsten naar analogie met andere vormen van nesten. Nesten kan
uiteraard arbitrair diep gebeuren.
Onderstaand experimentje toont een lijst life van drie elementen.
Ieder element is op zich weer een lijstje van twee elementen. De lijst
stelt een lijst van landen voor samen met hun gemiddelde
levensverwachting. We zien dat het indexeren van life op posities \(0\),
\(1\) en \(2\) telkens een lijstje van twee elementen weergeeft. De twee
laatste experimenten laten zien hoe een geneste lijst in één slag
geïndexeerd kan worden d.m.v. indexen die mekaar opeenvolgen, telkens
met vierkante haken errond. Zo geeft de expressie life[0][1] de eerste
component van de nulde component van de lijst weer die geassocieerd is
met de variabele life.
life = [['Canada' , 76.5], ['United States' , 75.5], ['Mexico' , 72.0]]
life[0]
['Canada', 76.5]
life[1]
['United States', 75.5]
life[2]
['Mexico', 72.0]
life[0][0]
'Canada'
life[0][1]
76.5
Men kan ook lijsten en tupels vrij mengen met elkaar. Hier volgt een voorbeeld van een lijst die data over ons zonnestelsel bijhoudt:
planets = [("Mercury",0.3871,0.053,4840,0.241,58.79, []),
("Venus",0.7233,0.815,12200,0.615,-243.68, []),
("Earth",1.0000,1.000,12756,1.000,1.00,
[("Moon",3476,0,"")]),
("Mars",1.5237,0.109,6790,1.881,1.03,
[("Phobos",22,1877,"Hall"),
("Deimos",8,1610,"Hall")]),
("Jupiter",5.2028,317.900,142800,11.862,0.41,
[("Io",3550,1610,"Galilei"),
("Europa",3100,1610,"Galilei"),
("Ganymedes",5600,1610,"Galilei"),
("Callisto",5050,1610,"Galilei")]),
("Saturn",9.5388,95.100,119300,29.458,0.43,
[("Mimas",520,1789,"Herschel"),
("Enceladus",600,1789,"Herschel"),
("Tethys",1200,1684,"Cassini"),
("Dione",1300,1684,"Cassini"),
("Rhea",1300,1672,"Cassini"),
("Titan",4950,1655,"Huygens"),
("Hyperion",400,1848,"Bond"),
("Japetus",1200,1671,"Cassini"),
("Phoebe",300,1898,"Pickering"),
("Janus",350,1966,"Dolfus")]),
("Uranus",19.1819,14.500,47100,84.013,-0.45,
[("Ariel",600,1851,"Lassell"),
("Umbriel",400,1851,"Lassell"),
("Titania",1000,1787,"Herschel"),
("Oberon",800,1787,"Herschel"),
("Miranda",100,1948,"Kuiper")]),
("Neptune",30.0578,17.500,44800,164.793,0.63,
[("Triton",4000,1846,"Lassell"),
("Nereide",300,1949,"Kuiper")])]
De variabele planets bevat een lijst van \(8\) tupels. Ieder tupel
is een \(7\)-tupel waarvan de laatste component opnieuw een lijst is. De
betekenis van het tupel is: de naam van een planeet, de afstand van de
planeet tot de zon, het aantal aardmassa’s dat de planeet zwaar is,
de diameter van de planeet, de tijd die nodig is voor een omwenteling
rond de zon, de tijd die nodig is voor een omwenteling om haar as en
tenslotte een lijst van haar manen. Iedere maan wordt voorgesteld door
een tupel bestaande uit de naam van de maan, haar diameter, het jaar van
ontdekking en de naam van haar ontdekker.
Het indexeren in de lijst levert dan als resultaat een \(7\)-tupel. En het laatste element van dat \(7\)-tupel is een lijst van manen.
planets[3]
('Mars',
1.5237,
0.109,
6790,
1.881,
1.03,
[('Phobos', 22, 1877, 'Hall'), ('Deimos', 8, 1610, 'Hall')])
planets[3][6]
[('Phobos', 22, 1877, 'Hall'), ('Deimos', 8, 1610, 'Hall')]
Op dit ogenblik ziet het ernaar uit dat tupels en lijsten zeer gelijkaardig zijn. Maar er zijn belangrijke verschillen in de bewerkingen die mogelijk zijn. Dat wordt verderop uit de doeken gedaan.
Ingebouwde Operatoren en Functies¶
Python bevat een aantal ingebouwde operatoren en functies die we kunnen
gebruiken om lijsten te manipuleren, zonder dat we daarvoor bibliotheken
hoeven te importeren. Hieronder zien we hoe de (herinner, overladen) +
operator twee lijsten aan mekaar plakt. Hierbij wordt een nieuwe lijst
gevormd die bestaat uit twee “deellijsten” die corresponderen met de
originele operanden van de + operator.
original = ['H' , 'He' , 'Li' ]
final = original + ['Be']
final
['H', 'He', 'Li', 'Be']
original
['H', 'He', 'Li']
original + 'Be'
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-22-879b45cec85f> in <module>
----> 1 original + 'Be'
TypeError: can only concatenate list (not "str") to list
Het vierde experimentje laat een interessante fout zien: de + operator
voor lijsten verwacht twee lijsten en dus niet een lijst en een string.
Dat is ook wat de foutmelding weergeeft.
Er bestaan redelijk veel ingebouwde operatoren die toepasbaar zijn op
lijsten. Het is beslist niet de bedoeling dat je ze van buiten gaat
leren. Indien je echter een vrij simpele en repetitieve opdracht op
lijsten nodig hebt is de kans wel groot dat die al in Python aanwezig
is. Je moet dus wél de reflex hebben om er eerst de Python documentatie
op na te slaan alvorens zélf aan het programmeren te slaan. Hieronder
laten we bijvoorbeeld de overladen operator * zien. Deze verwacht in
dit geval een lijst en een geheel getal. Hij geeft een lijst weer die uit
precies zoveel “kopies” van de lijst bestaat als het getal weergeeft.
l1 = [1,2,3]
l1*3
[1, 2, 3, 1, 2, 3, 1, 2, 3]
Ten slotte bespreken we een aantal ingebouwde functies die we op lijsten kunnen toepassen. Deze nemen meestal een lijst als argument en produceren een getal als resultaat. Hieronder enkele voorbeelden van functies die je beslist dient te onthouden:
half_lives = [87.74, 24110.0, 6537.0, 14.4, 376000.0]
len(half_lives)
5
max(half_lives)
376000.0
min(half_lives)
14.4
sum(half_lives)
406749.14
Zoals verwacht berekent len de lengte van een lijst. max en min
berekenen respectievelijk het grootste en het kleinste element van de
lijst. Sommige van deze functies zijn overigens niet alleen toepasbaar
op lijsten van getallen. Zoals we hieronder zien zijn max (en ook
min) bijvoorbeeld ook toepasbaar op lijsten van strings. Voor sum is
dat dan weer niet het geval. Merk op dat de foutmelding die we in dit
geval krijgen niet meteen veelzeggend is.
max(["a", "b", "c"])
'c'
sum(["a", "b", "c"])
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-30-37b60a2644ea> in <module>
----> 1 sum(["a", "b", "c"])
TypeError: unsupported operand type(s) for +: 'int' and 'str'
Slicing¶
Met indexering is het mogelijk om één welbepaalde plaats van een lijst op te vragen. Het resultaat van het indexeren is de waarde die op die plaats in de lijst zit. Python laat echter ook toe om hele deellijsten tegelijk vast te pakken. In dat geval spreken we niet van indexeren maar van slicing. Met slicing kunnen we als het ware van een lijst verschillende “sneetjes” snijden. Hieronder een voorbeeld.
nineties = [ 1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999]
nineties
[1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999]
early_nineties = nineties[1:4]
early_nineties
[1991, 1992, 1993]
nineties
[1990, 1991, 1992, 1993, 1994, 1995, 1996, 1997, 1998, 1999]
We vertrekken met een lijst nineties die 10 elementen bevat. Met de
uitdrukking nineties[1:4] “snijden we de elementen vanaf index 1 tot
(maar zonder) 4 uit de lijst”. De laatste lijn laat echter zien dat dit
de originele lijst niet kapot maakt. De slice is dus een kopie van een
stuk van de oorspronkelijke lijst.
De volgende experimenten laten zien wat er gebeurt indien we één van beide grensindices van de slice achterwege laten. Een slice die begint met een dubbele punt begint vooraan de lijst. Een slice die eindigt met een dubbele punt loopt tot het einde van de lijst. Negatieve grenswaarden beginnen zoals steeds te tellen van achteraan de lijst.
nineties[:4]
[1990, 1991, 1992, 1993]
nineties[4:]
[1994, 1995, 1996, 1997, 1998, 1999]
nineties[:-4]
[1990, 1991, 1992, 1993, 1994, 1995]
nineties[-7:]
[1993, 1994, 1995, 1996, 1997, 1998, 1999]
Mutatie van lijsten¶
Het grote verschil tussen lijsten en tupels is dat we bestaande lijsten
kunnen veranderen daar waar dit met tupels niet kan. Dit betekent dat
ieder tupel een stukje data is dat in ons computergeheugen opgeslagen
zit en waarvan de componenten na het aanmaken (m.b.v. een expressie met
ronde haken) niet meer kunnen veranderd worden. Met lijsten is dat
anders. We kunnen dus een lijst aanmaken (m.b.v. een expressie met
vierkante haken) en nadien één van de componenten veranderen zonder
dat daarbij een nieuwe lijst wordt gemaakt. Dat doen we met de volgende
syntactische vorm. Deze gelijkt sterk op de gewone assignment. Het
verschil is dat er geen variabele maar een lijst indexering staat aan de
linkerkant van het = teken.
Hieronder zien we meteen een voorbeeld. We maken een lijst van
edelgassen (in Python zijn dat gewoon strings) en we realiseren ons pas
nadien dat we ons mistypt hebben en ’noon’ in plaats van ’neon’
hebben gebruikt als string op index 1. Dat kunnen we eenvoudig aanpassen
met het statement nobles[1] = ’neon’. De laatste lijn laat zien dat
dit daadwerkelijk de originele lijst heeft aangepast.
nobles = ['helium' , 'noon' , 'argon' , 'krypton' , 'xenon' , 'radon' ]
nobles
['helium', 'noon', 'argon', 'krypton', 'xenon', 'radon']
nobles[1] = 'neon'
nobles
['helium', 'neon', 'argon', 'krypton', 'xenon', 'radon']
Men zegt dat lijsten muteerbaar zijn daar waar tupels en strings niet muteerbaar zijn. Op het eerste zicht lijkt dit misschien niet zo nuttig: we moeten maar zien dat we geen fouten typen! Later zullen we echter zien dat zeer veel toepassingen direct steunen op de muteerbaarheid van lijsten. Stel dat we bijvoorbeeld een lijst maken met meetwaarden en dat we deze willen sorteren van klein naar groot. In een later topic zullen we Python functies schrijven die de elementen van een lijst kunnen sorteren door ze herhaaldelijk onderling van plaats te verwisselen. Hiervoor dient het uiteraard mogelijk te zijn dat we de elementen van een lijst kunnen veranderen.
Alias versus Kopie¶
Van zodra we lijsten beginnen aan te passen moeten we zeer goed
opletten. Dit is bijzonder waar indien we twee (of meerdere) variabelen
hebben die met dezelfde lijst geassocieerd zijn. Beschouw hieronder de
lijst dutch van Nederlandstalige speelkaarten. Door het statement
english = dutch maken we geen kopie van die lijst maar introduceren we
gewoon een nieuwe variabele die eveneens met die lijst geassocieerd
wordt. Dat komt doordat een assignment statement zoals steeds de
waarde van de rechterkant (de lijst dus) associeert met de variabele
aan de linkerkant. We hebben nu 2 variabelennamen die beide “wijzen
naar” dezelfde lijst. We zeggen dat de tweede naam (english dus) een
alias is voor de eerste naam. Dat wordt bijzonder zichtbaar als we de
lijst english beginnen aan te passen. Zoals getoond wordt in de
laatste expressie hebben we de originele lijst aangepast!
dutch = ["aas",2,3,4,5,6,7,8,9,"boer","dame","heer"]
english = dutch
english[0] = "ace"
english[9] = "jack"
english[10] = "queen"
english[11] = "king"
dutch
['ace', 2, 3, 4, 5, 6, 7, 8, 9, 'jack', 'queen', 'king']
english
['ace', 2, 3, 4, 5, 6, 7, 8, 9, 'jack', 'queen', 'king']
Indien we geen alias maar een echte kopie van een lijst willen, dan
gebruiken we in Python het bijzonder handige truukje van slicing zonder
grensindices. Het statement english = dutch[:] associeert de
variabele english met een kopie van de originele lijst. Dat wordt
aangetoond in de laatste twee lijnen van het experiment. De
veranderingen die we aan de lijst english hebben aangebracht hebben de
originele lijst dutch niet aangetast.
dutch = ["aas",2,3,4,5,6,7,8,9,"boer","dame","heer"]
english = dutch[:]
english[0] = "ace"
english[9] = "jack"
english[10] = "queen"
english[11] = "king"
dutch
['aas', 2, 3, 4, 5, 6, 7, 8, 9, 'boer', 'dame', 'heer']
english
['ace', 2, 3, 4, 5, 6, 7, 8, 9, 'jack', 'queen', 'king']
Maken van Lijsten¶
Nu we weten wat een lijst is, bestuderen we systematisch hoe we in
Python lijsten kunnen bouwen. We bespreken drie manieren: door
opsomming, door constructie m.b.v. de range functie en door omschrijving m.b.v.
zogenoemde list comprehensions.
Door Opsomming¶
De eerste manier bestaat er gewoon in de elementen van de lijst op te sommen. Dit is uiteraard gewoon wat we tot nu toe gedaan hebben. De syntaxregels van Python schrijven voor dat we de elementen opsommen, gescheiden door komma’s en dat we vierkante haken gebruiken om de lijst af te bakenen:
['helium' , 'neon' , 'argon' , 'krypton' , 'xenon' , 'radon']
['helium', 'neon', 'argon', 'krypton', 'xenon', 'radon']
Merk op dat het maken van de lijst conceptueel iets anders is dan het associëren van die lijst aan een variabele. Indien we onze lijst een naam willen geven, gebruiken we zoals vanouds een toekenning:
nobles = ['helium' , 'neon' , 'argon' , 'krypton' , 'xenon' , 'radon']
nobles
['helium', 'neon', 'argon', 'krypton', 'xenon', 'radon']
De range functie¶
Dikwijls hebben we zeer reguliere lijsten nodig zoals “alle getallen van
1 tot 5” of “alle getallen van 0 tot 100 met sprongen van 20”. Om ons al
het tikwerk te besparen om zulke lijsten met de hand op te moeten
sommen, bestaat er in Python de zeer handige range functie. Dit is een
ingebouwde functie waarvan sommige argumenten verplicht zijn en andere
optioneel zijn. Je kan via de range functie een lijst bouwen door in de oproep van range de grenzen en stap op te geven en dan door een oproep van list te dwingen van het bekomen resultaat in een lijst te zetten.
Hier volgen een reeks experimenten:
list(range(1,5))
[1, 2, 3, 4]
list(range(0))
[]
list(range(1,10,2))
[1, 3, 5, 7, 9]
list(range(0,100,20))
[0, 20, 40, 60, 80]
list(range(0,100,-20))
[]
list(range(100,0,-20))
[100, 80, 60, 40, 20]
De eerste twee argumenten duiden de grenzen aan van de lijst in opbouw.
Merk op dat het tweede argument zélf niet wordt opgenomen (t.t.z.
range(1,5) gaat slechts tot en met \(4\)). Indien we het eerste argument
weglaten (bijvoorbeeld in range(5)) veronderstelt Python dat we
sowieso vanaf nul willen beginnen. Indien er géén derde argument
meegegeven wordt, worden álle tussenliggende elementen in de lijst
opgenomen. Indien er echter wél een derde argument wordt meegegeven, dan
bepaalt dit de stapgrootte waarmee tussenliggende elementen worden
gegenereerd. We gebruiken een negatieve stapgrootte om af te tellen.
De range functie heeft conceptueel niet zoveel om het lijf. Het is
gewoon een zeer handige manier om met weinig tekst vrij lange lijsten te
construeren. Dit lukt uiteraard alleen maar als het om reguliere lijsten
gaat waarvan de afstand tussen 2 opeenvolgende elementen een constante
is.
Met Comprehensions¶
Alhoewel een lijst geen wiskundige verzameling is (elementen kunnen immers meerdere keren voorkomen), is het toch nuttig even de parallel met verzamelingen te trekken. In de wiskunde kunnen we een verzameling neerschrijven door opsomming (t.t.z. door de elementen op te sommen) of door omschrijving. Dat laatste bestaat uit het neerschrijven van een voorschrift dat bepaalt welke elementen wél en welke eventueel niet in de verzameling worden opgenomen. Zo kunnen we bij voorbeeld de verzameling van de even natuurlijke getallen omschrijven als \(\{ 2x | x \in \mathbf{N} \}\). Deze techniek wordt ook door Python ondersteund om lijsten aan te maken. Hieronder zien we een voorbeeld waarbij we een lijst aanmaken van alle even getallen tussen \(0\) en \(10\). Zo’n expressie wordt een list comprehension genoemd.
[ i * 2 for i in range(0,6) ]
[0, 2, 4, 6, 8, 10]
Een list comprehension bestaat uit een expressie (hier: i * 2) die de
elementen van de lijst beschrijft. De variabelen in deze expressie mogen
uit de omringende context komen of uit de generatoren die in de
comprehension zijn opgenomen. Iedere generator beschrijft waarden die
“gegenereerd” worden m.b.v. een for...in... expressie. Bovenstaand
voorbeeld heeft slechts één generator maar we zullen zo meteen ook
voorbeelden zijn met meerdere generatoren. Eerst nog enkele voorbeelden
die de kracht van list comprehensions aantonen.
[ x**2 for x in range(10) ]
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
[ x**3 for x in range(10) ]
[0, 1, 8, 27, 64, 125, 216, 343, 512, 729]
[ 2**i for i in range(10) ]
[1, 2, 4, 8, 16, 32, 64, 128, 256, 512]
In bovenstaande voorbeelden werd telkens de rangefunctie gebruikt als generator. Je kan ook een lijst, tupel of string als generator gebruiken. Hieronder nog een paar voorbeelden.
[ i*2 for i in [4,1,7,3,9,2,5,8,7,1] ]
[8, 2, 14, 6, 18, 4, 10, 16, 14, 2]
[ len(w) for w in ["The","quick","brown","fox","jumps","over","the","lazy","dog"] ]
[3, 5, 5, 3, 5, 4, 3, 4, 3]
[ i*2 for i in (0,1,2,3) ]
[0, 2, 4, 6]
[ i*2 for i in "Viviane" ]
['VV', 'ii', 'vv', 'ii', 'aa', 'nn', 'ee']
Meerdere Generatoren
Je kan meerdere generatoren na elkaar gebruiken. In het eerste voorbeeld hieronder wordt een lijst
geconstrueerd van alle koppels (i,j) waarbij i en j door een verschillende generator bepaald zijn. I.h.a. laat het gebruik van meerdere generatoren toe om de elementen van de lijst die je aan het construeren bent te beschrijven aan de hand van meerdere variabelen.
[ (i,j) for i in range(1,4) for j in ['a','b'] ]
[(1, 'a'), (1, 'b'), (2, 'a'), (2, 'b'), (3, 'a'), (3, 'b')]
In het voorbeeld hieronder zal de expressie (soort,rang)
geëvalueerd worden (en dus een tupel maken) voor alle waarden die uit de
generatoren komen. De eerste generator zegt dat soort zal variëren
tussen "klaveren" en "harten". Voor elk van deze waarden zal de
volgende generator geëvalueerd worden. Deze laat rang variëren van
"aas" tot "zot". Aan de volgorde waarin de koppels in de
lijst terecht komen kan je begrijpen in welke volgorde de opeenvolgende
generatoren worden uitgevoerd.
[ (soort,rang)
for soort in ("klaveren", "schoppen", "ruiten", "harten")
for rang in ("aas","heer","dame","zot") ]
[('klaveren', 'aas'),
('klaveren', 'heer'),
('klaveren', 'dame'),
('klaveren', 'zot'),
('schoppen', 'aas'),
('schoppen', 'heer'),
('schoppen', 'dame'),
('schoppen', 'zot'),
('ruiten', 'aas'),
('ruiten', 'heer'),
('ruiten', 'dame'),
('ruiten', 'zot'),
('harten', 'aas'),
('harten', 'heer'),
('harten', 'dame'),
('harten', 'zot')]
De algemene regel bij verschillende generatoren is dus dat iedere generator volledig uitgevoerd wordt voor iedere waarde van de generator die er links van staat. Indien we drie generatoren hebben die respectievelijk \(5\), \(10\) en \(20\) elementen opleveren, dan zal de expressie van de list comprehension in totaal \(1000\) keer uitgevoerd worden en zal onze opgebouwde lijst dus ook \(1000\) elementen bevatten.
Filters
Naast generatoren kan een list comprehension ook zogenoemde filters
bevatten. Dit zijn elementen van de vorm if expressie. De filters
worden geëvalueerd en laten enkel waarden “passeren” waarvoor de
expressie True oplevert.
Enkele envoudige voorbeelden illustreren het idee.
[ i for i in [4,1,7,3,9,2,5,8,7,1] if i>5 ]
[7, 9, 8, 7]
[ w for w in ["The","quick","brown","fox","jumps","over","the","lazy","dog"] if len(w) == 4 ]
['over', 'lazy']
[ (i,j) for i in range(0,5) for j in range(0,5) if i==j ]
[(0, 0), (1, 1), (2, 2), (3, 3), (4, 4)]
Geneste Comprehensions
We kunnen geneste lijsten kunnen bouwen
m.b.v. geneste list comprehensions. Dat zijn list comprehensions
waarvan de expressie zélf weer een list comprehension is. Deze geneste list
comprehension zal geëvalueerd worden voor ieder element van de buitenste
comprehension. Het volgende voorbeeld genereert op deze manier een lijst van 3 lijsten die elk 5 tupels (i,j) bevatten. Telkens de geneste comprehension wordt uitgevoerd, wordt er dus een lijst van 5 koppels gegenereerd. De buitenste
comprehension zorgt ervoor dat er zo 3 lijsten aangemaakt worden.
[ [ (i,j) for i in range(0,5) ] for j in range(0,3) ]
[[(0, 0), (1, 0), (2, 0), (3, 0), (4, 0)],
[(0, 1), (1, 1), (2, 1), (3, 1), (4, 1)],
[(0, 2), (1, 2), (2, 2), (3, 2), (4, 2)]]
Het tweede voorbeeld hieronder bouwt de nulmatrix met zo’n geneste list comprehension. De geneste comprehension bouwt een lijst van 5 nullen. De buitenste comprehension bouwt zo 5 lijsten.
[ [ 0 for i in range(0,5) ] for i in range(0,5) ]
[[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]]
Het volgende voorbeeld toont een functie die een een eenheidsmatrix construeert. De vierkante matrix heeft overal nullen behalve op de diagonaal waar enen staan. De
eerste functie elm is een kleine hulpfunctie.
def elm(i,j):
if i==j:
return 1
else:
return 0
def make_diagonal_matrix(n):
return [ [elm(i,j) for i in range(0,5) ] for j in range(0,5) ]
make_diagonal_matrix(5)
[[1, 0, 0, 0, 0],
[0, 1, 0, 0, 0],
[0, 0, 1, 0, 0],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 1]]
Geneste comprehensions versus meerdere generatoren
Let goed op, meerdere generatoren na elkaar levert een fundamenteel ander resultaat dan geneste comprehensions.
Onderstaand voorbeeld genereert suites van kaarten van dezelfde soort. In elke deellijst zitten “aas”,”heer”,”dame” en “zot” van dezelfde kaartsoort. De buitenste generator zegt dat soort zal variëren
tussen "klaveren" en "harten". Voor elk van deze waarden wordt de binneste geneste comprehension geëvalueerd. De binnenste generator laat rang variëren van "aas" tot "zot".
[ [(soort,rang)
for rang in ("aas","heer","dame","zot")]
for soort in ("klaveren", "schoppen", "ruiten", "harten")]
[[('klaveren', 'aas'),
('klaveren', 'heer'),
('klaveren', 'dame'),
('klaveren', 'zot')],
[('schoppen', 'aas'),
('schoppen', 'heer'),
('schoppen', 'dame'),
('schoppen', 'zot')],
[('ruiten', 'aas'),
('ruiten', 'heer'),
('ruiten', 'dame'),
('ruiten', 'zot')],
[('harten', 'aas'),
('harten', 'heer'),
('harten', 'dame'),
('harten', 'zot')]]
Maar in een eerder voorbeeld met 2 generatoren dat we hier hernemen krijgen we een we een lijst met 16 speelkaarten en dus niet een lijst met 4 deellijsten die elk 4 kaarten bevatten van dezelfde soort.
[ (soort,rang)
for soort in ("klaveren", "schoppen", "ruiten", "harten")
for rang in ("aas","heer","dame","zot") ]
[('klaveren', 'aas'),
('klaveren', 'heer'),
('klaveren', 'dame'),
('klaveren', 'zot'),
('schoppen', 'aas'),
('schoppen', 'heer'),
('schoppen', 'dame'),
('schoppen', 'zot'),
('ruiten', 'aas'),
('ruiten', 'heer'),
('ruiten', 'dame'),
('ruiten', 'zot'),
('harten', 'aas'),
('harten', 'heer'),
('harten', 'dame'),
('harten', 'zot')]
Geavanceerde Voorbeelden
Met list comprehensions kan je zeer ingewikkelde lijsten toch op zeer compacte en elegante wijze neerschrijven. Een eerste voorbeeld bestaat uit het berekenen van alle drietallen \((a,b,c)\) met \(a, b, c \in \{1,...,100\}\) zodanig dat \(a^2+b^2=c^2\). Dat is eigenlijk heel eenvoudig. We schrijven een list comprehension waarvan de expressie een drietal is in de vorm van een Python tupel. Dan volgen er 3 generatoren om alle combinaties te genereren en een filter die alleen de gewenste combinaties “doorlaat”.
[ (a,b,c)
for a in range(1,10)
for b in range(1,10)
for c in range(1,10)
if a**2 + b**2 == c**2]
[(3, 4, 5), (4, 3, 5)]
Een tweede geavanceerd voorbeeld creëert een lijst van alle
priemgetallen tussen 1 en 50. Deze wordt gegenereerd in twee stappen.
Eerst maken we de lijst noprimes. We laten i variëren tussen \(2\) en
\(7\). En voor elke i laten we j variëren tussen het 2-voud van i
tot maximum \(50\), en dit in stappen van i. Met andere woorden, j
varieert tussen \(2i\), \(3i\), \(4i\), enzovoort. De lijst noprimes bevat
dus alle “j-vouden” (\(j \geq 2\)) van alle \(i\)’s.
noprimes = [j for i in range(2, 8) for j in range(i*2, 50, i)]
De lijst primes
wordt dan zeer makkelijk gedefinieerd als alle getallen x tussen \(2\)
en \(50\) die niet in deze lijst voorkomen. Priemgetallen zijn immers
enkel deelbaar door \(1\) en zichzelf, en dus “geen enkel j-voud”. Hier
zien we het resultaat:
primes = [x for x in range(2, 50) if x not in noprimes]
primes
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
Het laatste geavanceerde voorbeeld bestaat uit het schrijven van een
functie delers die een lijst weer geeft met alle delers van het
argument n. De functie genereert alle d waarden tussen \(2\) en \(n\).
Enkel de waarden waarvoor de rest bij deling door d nul is worden
doorgelaten. Dat zijn immers de delers.
def delers(n):
return [ d for d in range(2,n) if n % d == 0]
Hier zien we de functie twee keer aan het werk om de delers van 16 en die van 11 te berekenen. Vermits 11 een priemgetal is, heeft het geen delers en krijgen we zoals verwacht de lege lijst weer.
delers(16)
[2, 4, 8]
delers(11)
[]
Opmerking
Merk op dat een filter van de vorm if conditie is. Dat is uiteraard
zeer gerelateerd aan het if statement dat we al eerder gezien
hebben. Toch is het belangrijk beide goed uit elkaar te houden. De vorm
van if die we hier gezien hebben komt enkel voor in list
comprehensions. Het if statement komt voor in de body van functies en
kan bovendien nog optionele elif en else clausules bevatte. Dat is
niet het geval voor filters in list comprehensions.
Gevalstudie: Matplotlib¶
In een eerdere sectie hebben we getoond hoe we met de Matplotlib
bibliotheek grafiekjes kunnen plotten. Dat was soms nogal omslachtig
aangezien we de functie plot met een tupel dienden op te roepen en we
alle componenten van dat tupel dus één voor één dienden in te tikken.
In deze sectie pikken we de draad met Matplotlib terug op. In plaats van
plot op te roepen met een tupel mogen we ze ook oproepen met een
lijst. De bedoeling is nu van die lijst niet te maken door alle
elementen ervan handmatig op te sommen, maar juist de kracht van list
comprehensions hiervoor te gebruiken. Dat zien we hieronder.
import matplotlib.pyplot as plt
from math import *
plt.plot([ x**2 for x in range(1,100)], label = 'square')
plt.plot([ 40*log(x) for x in range(1,100)], label = "40*log")
plt.plot([ 30*x+10 for x in range(1,100)], label = "30x+10")
plt.legend()
plt.show()
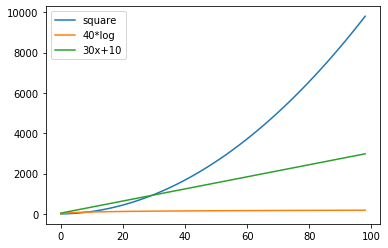
De 3 list comprehensions verschillen in de
expressie die ze gebruiken om de gewenste lijst te genereren. In het
eerste geval worden kwadraten gegenereerd. In het tweede geval worden
logaritmen (maal 40) gegenereerd. In het derde geval worden lineaire
waarden van de vorm \(30x+10\) gegenereerd. In elk van de gevallen levert
dat dus een lijst (van 100 getallen) op die
aan plot wordt meegegeven. Door list comprehensions
te gebruiken hebben we ons dus enorm veel tikwerk bespaard. Zonder
comprehensions hadden we 3 keer 100 waarden moeten opsommen!
Het gebruikt van de optionele parameter label bij de oproep van plot in combinatie met het oproepen van legend zorgt voor de kleine legende in de plot.
De oproepen van show in de laatste lijn zorgt dat Matplotlib
een venster open doet om de (in het computergeheugen) getekende plots
ook effectief te tonen.
In de topic over recursieve functies hebben we zulke plots gebruikt om functies te profilen.
Een simpele plot die bv. uitzet hoelang het duurt om fac(n) te berekenen voor oplopende waarden van n
kan uitgezet worden door onderstaande code. Eem simpele comprehension vergaart 50 metingen en die worden uitgeplot.
import time
def fac(n):
if (n == 0):
return 1
else:
return n * fac (n-1)
def timed_fac(n):
t1 = time.time()
fac(n)
t2 = time.time()
return (t2-t1) * 1000
serie = [timed_fac(n) for n in range(50)]
plt.plot(serie, "^g")
plt.show()

Je ziet een plot die een lineair verband suggereert. Er zijn onregelmatigheden en uitschieters mogelijk omdat je computer heel veel dingen tegelijk aan het doen is, bv. naar je toetsenbord luisteren, mail binnenhalen, een autosave van een bestand doen, etc. Je kan de plot een aantal keer na elkaar maken en je kan grote verschillen zien.
Om uitschieters die het gevolg zijn van het feit dat je computer op een bepaald moment ook nog iets anders aan het doen is (bv. mail binnenhalen) te vermijden, is een naief idee om voor elke n de tijd om fac(n) te berekenen 100 keer te timen en dan een gemiddelde uit te plotten. Dat gebeurt door onderstaande geneste comprehension. De buitenste generator varieert de n, de binnenste generator loopt 100 keer.
serie_of_avg = [sum([timed_fac(n) for i in range (100)])/100 for n in range(50)]
plt.plot(serie_of_avg, "^b")
plt.show()
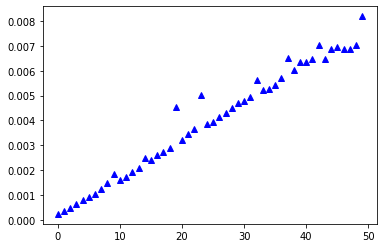
Waar je zou verwachten dat het de grafiek iets gladder maakt omdat je een gemiddelde neemt over 100 keer meten voor elke waarde van n i.p.v. 1 keer meten is dat niet noodzakelijk zo. Je doet de 100 metingen voor een bepaalde n ook vlak na elkaar omdat n uit de buitenste generator komt. Als je computer op dat moment net mail aan het binnenhalen is zullen die opeenvolgende metingen met grote kans ook allemaal abnormaal groot zijn.
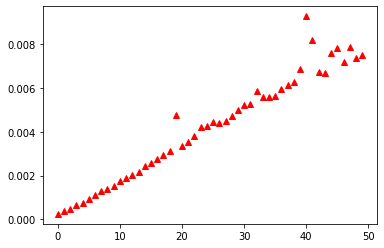
Een nog ingewikkelder idee is om te profilen door 100 keer te meten met n variërend van 0 tot 50 wat een tabel van meetwaarden oplevert. Die tabel is een geneste lijst met 50 deellijsten van elk 100 metingen.
Met een slimme comprehension kan je dan het gemiddelde berekenen van alle meetwaarden op de overeenkomstige plaatsen van die deellijsten. Het binnenhalen van mail op een bepaald moment zal nu storend werken op het timen van een reeks metingen waarbij n variëert. Zoals je ziet blijven er pieken. De vertraging die optreed omdat je computer iets anders aan het doen is kan zo groot zijn t.o.v. van de heel korte tijd die je computer nodig heeft om wat rekenwerk te doen dat er pieken blijven komen omdat enkele slechte metingen door hun relatieve grootte het gemiddelde blijven verstoren. Het profilen van code door tijdsmetingen te doen moet eigenlijk gebeuren op speciale apparatuur die al die inferenties uitschakelt.
series = [[timed_fac(n) for i in range(100)] for n in range(50)]
averaged = [sum([series[n][i] for i in range(100)])/100 for n in range(50)]
plt.plot(averaged, "^r")
plt.show()
Lijsten Verwerken met Recursie¶
Indien je alle elementen van een bestaande lijst wil aflopen om op basis hiervan een nieuwe lijst te bouwen (zoals bij voorbeeld een lijst van kwadraten van alle getallen van 1 tot 100) zijn list comprehensions uitermate geschikt. Indien je echter alle elementen wil verwerken zonder dat dat een nieuwe lijst moet opleveren hebben we andere technieken nodig. In wat volgt leggen we ons toe op twee problemen, namelijk het bepalen van de som van alle getallen in een lijst en het bepalen van het kleinste getal in een lijst met getallen.
We beginnen met het berekenen van de som van de getallen in een lijst. Vergeet eventjes dat de functie sum bestaat in Python, we schrijven hier een
eigen versie om iets uit te leggen. Van een lege lijst weten we dat de som van alle elementen 0 is.
Als een lijst niet leeg is kunnen we de som berekenen door het eerste element op te tellen bij de som van de rest van de lijst.
Hieronder zien we een functie my_sum die dat doet.
my_sum roept een hulpfunctie sum_aux op. sum_aux is een recursieve functie die de hele lijst
“afwandelt” door een indextellertje idx dat bij 0 begint doorheen de recursie op te
hogen tot de lengte van de lijst bereikt is. Dat tellertje wordt
gebruikt om de lijst op de juiste plaats te indexeren (lst[idx]) en
het bijhorende element te tellen bij de som van de rest van de lijst. De som van de rest van de lijst wordt berekend door de recursieve oproep waarin de idx wordt opgehoogd.
def my_sum(lst):
return sum_aux(lst,0)
def sum_aux(lst,idx):
if idx == len(lst):
return 0
else:
return lst[idx] + sum_aux(lst,idx+1)
min([1,4,3])
1
my_sum([1,2,3,4,5])
15
Ons tweede voorbeeld zoekt het kleinste getal in een lijst.
Vergeet opnieuw eventjes dat de functies min en max bestaan.
Ook hier
zullen we de lijst “aflopen” m.b.v. recursie. Hieronder zien we de
functie smallest die een lijst als argument neemt. Deze functie roept
meteen de hulpfunctie smallest_aux op met drie argumenten: de lijst,
het eerste element van de lijst en het getal \(1\). De eerste parameter is
de lijst die doorheen de hele recursie getransporteerd wordt. De tweede
parameter sma is “de kleinste tot nu toe” en idx is opnieuw een
teller die aangeeft welk element van de lijst we aan het bekijken zijn.
smallest_aux geeft sma als resultaat terug indien we op het einde
van de lijst beland zijn (t.t.z. idx = len(lts)). Indien het “huidige”
element van de lijst lst[idx] kleiner is dan de kleinste tot nu toe,
zoeken we verder vanaf de volgende positie idx+1 met lst[idx]
als nieuwe kleinste tot nu toe. Anders zoeker we verder vanaf de
volgende positie idx+1 maar behouden we sma als kleinste tot nu toe.
def smallest(lst):
return smallest_aux(lst,lst[0],1)
def smallest_aux(lst,sma,idx):
if idx == len(lst):
return sma
elif lst[idx] < sma:
return smallest_aux(lst,lst[idx],idx+1)
else:
return smallest_aux(lst,sma,idx+1)
smallest([3,5,2,1,4])
1
Lijsten Verwerken met het for Statement¶
In beide voorbeelden dienen we de lijst “af te lopen” en ieder elementje
van de lijst “vast te pakken” om er iets mee te doen. Dat doen we door
een indexteller idx doorheen de recursie te transporteren zodat we
alle elementen één voor één kunnen vastpakken met een expressie
lst[idx]. Dat kan veel eenvoudiger dank zij het zogenoemde for
statement van Python.
Opmerking: In wat volgt dien je even de for van de list
comprehensions te vergeten. Beide vormen van for zijn gelijkaardig
(daarom heten ze ook alletwee for) maar zijn niet exact hetzelfde. De
for lus die we zodadelijk gaan uitleggen is een nieuw soort statement.
Net zoals bij de meeste constructies in Python kent het for statement
nogal wat varianten. De eenvoudigste algemene vorm van het for
statement ziet er als volgt uit:
Python zal bij het uitvoeren van dit statement alle elementen van de
lijst aflopen en deze één per één aan de gekozen variabele associëren.
Met een beetje verbeelding zou je deze Python constructie kunnen
vergelijken met
“\(\forall~\textrm{x} ~\in~\textrm{lijst}:~\textrm{doe iets met x}\)” in de
wiskunde. Het gegeven block zal dus worden herhaald voor elk van deze
associaties. Zo’n for statement wordt ook wel een “for lus” genoemd
(Eng.: loop). Het block wordt de “body van de lus” genoemd. Vermits het
block herhaaldelijk uitgevoerd wordt voor alle elementen van de lijst,
spreekt men over een iteratie.
Laat ons nu beide voorbeelden herschrijven m.b.v. de for constructie.
We beginnen met my_sum:
def my_sum(lst):
tot = 0
for e in lst:
tot = tot + e
return tot
my_sum([1,2,3,4,5])
15
Deze functie heeft een body block die uit 3 statements bestaat. We
definiëren eerst een lokale variabele tot met initiële waarde 0.
De som van alle elementen wordt berekend door de body van de for uit
te voeren voor alle elementen e uit de lijst. Telkens wordt tot
vervangen door de vorige waarde van tot, plus het huidige element e.
Op het einde geven we tot terug.
Ook smallest is te schrijven met een for constructie. We starten met
sma te initialiseren op het eerste element van de lijst. Vervolgens
nemen we alle indices idx tussen \(1\) en de lengte van de lijst. Indien
het element op positie idx daadwerkelijk kleiner is dan de kleinste
die we tot nu toe gevonden hebben (sma), vervangen we de kleinste tot
nu toe door dat element. Op het einde geven we sma gewoon terug.
def smallest(lst):
sma = lst[0]
for idx in range(1,len(lst)):
if lst[idx] < sma:
sma = lst[idx]
return sma
smallest([3,5,2,1,4])
1
Varianten van for: Enumereerbare Waarden¶
Het for statement werkt niet alleen voor lijsten. We kunnen er ook
alle elementen van een tupel mee aflopen of zelfs alle karakters van een
string. Hier is een voorbeeld dat het aantal klinkers in een gegeven
string telt:
def vowels(string):
count = 0
for letter in string:
if letter in ('a','e','i','o','u'):
count = count + 1
return count
vowels("het is goed weer vandaag")
9
Let goed op de structuur van de code. Het is een functie met een body
met 3 statements: een toekenning, een for lus en een return
statement. De for lus loopt alle letters van de gegeven string af. De
body van de for lust is een if statement waardoor alleen maar in
sommige stappen van de for lus de count wordt opgehoogd.
Ten slotte een gelijkaardig voorbeeld om aan te tonen dat for ook kan
gebruikt worden om de componenten van een tupel mee af te lopen. We
tellen het aantal componenten in een tupel dat gelijk is aan nul:
def zeroes(tuple):
count = 0
for el in tuple:
if el == 0:
count = count +1
return count
zeroes((3,1,0,4,2,6,3,0,5,9,0))
3
Zowel strings, tupels als lijsten noemen we enumereerbare waarden
omdat we ze één voor één kunnen “aflopen” in for lussen. Deze delen
een heel pak eigenschappen. Naast het for statement kunnen we ze
bijvoorbeeld ook gebruiken om te indexeren en om slices te berekenen.
Hieronder zien we enkele experimentjes die tonen dat we indexering en
slicing kunnen toepassen op strings. Bestudeer de voorbeelden in detail
zodat je begrijpt wat er aan de hand is.
rock = 'anthracite'
rock[9]
'e'
rock[0:3]
'ant'
rock[-5]
'a'
rock[-5:]
'acite'
for character in rock[:5]:
print (character)
a
n
t
h
r
Ook voor tupels kunnen we deze operatoren gebruiken.
bases = ('A', 'C', 'G', 'T')
for b in bases:
print(b)
A
C
G
T
bases[1:]
('C', 'G', 'T')
bases[1]
'C'
Samenvattend kunnen we stellen dat strings, tupels en lijsten drie types zijn waarmee we data kunnen “samenlijmen”. Een string kan enkel uit karakters (t.t.z. strings van lengte 1) bestaan maar een tupel en een lijst kan gelijk welke soort data bevatten. Lijsten en tupels zijn dus algemener dan strings. Lijsten zijn dan weer algemener dan tupels en strings omdat ze mutatie ondersteunen. De tabel hieronder laat zien welke constructie we kunnen gebruiken voor elk van de drie types.
Type |
|
Indexering |
Slicing |
Assignment |
|
|
|---|---|---|---|---|---|---|
|
\(\surd\) |
\(\surd\) |
\(\surd\) |
\(\varnothing\) |
\(\surd\) |
\(\surd\) |
|
\(\surd\) |
\(\surd\) |
\(\surd\) |
\(\varnothing\) |
\(\surd\) |
\(\surd\) |
|
\(\surd\) |
\(\surd\) |
\(\surd\) |
\(\surd\) |
\(\surd\) |
\(\surd\) |
Geneste for Lussen¶
Zoals de meeste Python constructies kunnen we ook for lussen in mekaar
nesten. Bij geneste for lussen spreken we doorgaans over een inner
loop en een outer loop. Dat hebben we bijvoorbeeld nodig om lijsten
af te lopen die zelf lijsten bevatten; t.t.z. om geneste lijsten (of
tupels en strings) af te lopen. Het onderstaande voorbeeld laat dit
zien. De functie min_max neemt een 2-dimensionale matrix als argument.
In Python kunnen we zulke matrices voorstellen als lijsten die zelf weer
lijsten bevatten. Zo kunnen we bijvoorbeeld de matrix:
in Python voorstellen als:
test = [[-4, 2, 8], [7, -13, 0], [0, 5, 9]]
test
[[-4, 2, 8], [7, -13, 0], [0, 5, 9]]
De functie min_max neemt zo’n matrix en geeft een 2-tupel terug dat
bestaat uit het kleinste en het grootste element van de matrix. Dit doen
we door alle elementen van iedere rij af te lopen. De body van min_max
bevat o.m. een for lus waarvan de body opnieuw een for lus is. Die
binnenste for lus wordt dus uitgevoerd voor elke waarde van de
buitenste for lus.
def min_max(mat):
sma = 0
lar = 0
for row in mat:
for el in row:
if el < sma:
sma = el
if el > lar:
lar = el
return (sma, lar)
Toegepast op bovenstaande matrix geeft dat:
min_max(test)
(-13, 9)
Geneste lussen zijn echter niet alleen nuttig om geneste lijsten mee af te lopen. Men kan er bvb. ook lijsten met zichzelf mee vergelijken. Het volgende voorbeeld is een functie die uit een lijst van getallen het getal weergeeft dat het vaakst voorkomt:
def most_frequent(lst):
frequence = 0
element = None
for el1 in lst:
count = 0
for el2 in lst:
if el1 == el2:
count = count + 1
if count > frequence:
element = el1
frequence = count
return element
most_frequent([3,1,0,4,2,6,3,0,5,9,0])
0
Deze functie loopt de lijst helemaal af en gaat voor elk el1 uit de
lijst de lijst opnieuw helemaal aflopen om te zien hoe vaak dat element
voorkomt in die lijst. Meteen hierna wordt er telkens weer getest of het
huidige element vaker voorkomt dat het element dat tot nu toe het vaakst
was voorgekomen. Indien dat het geval is vervangt het huidige element
het element dat tot nu toe het vaakst voorgekomen was. Op het einde
geven we terug hoe vaak het vaakst voorgekomen element voorkwam.
Iteratie en Lijsten: Gevalstudies¶
We hebben tot nu toe gezien dat we lijsten kunnen bouwen door de
elementen op te sommen, door de lijst te laten maken met een functie
zoals range of door de lijst te omschrijven m.b.v. een list
comprehension. Verder hebben we gezien dat we lijsten kunnen indexeren
en dat we hele stukken van lijsten kunnen selecteren m.b.v. slicing.
Verder kunnen we de elementen van een lijst veranderen m.b.v. een
assignment. Het for statement laat ons ten slotte toe om lijsten af te
lopen teneinde iets nuttigs te doen met de elementen die erin zitten.
In deze sectie bestuderen we twee gevalstudies uit de biologie. De
gevalstudies zijn beide simulaties van bestaande biologische processen.
De eerste gevalstudie laat zien hoe we de vorming van eiwitten kunnen
simuleren in Python. De tweede gevalstudie toont hoe we de aangroei van
populaties kunnen nabootsen. Beide gevalstudies maken gebruik van de
kracht van lijsten en van het for statement.
Gevalstudie 1: Simuleren van Eiwitexpressie¶
Een DNA-sequentie bestaat uit een opeenvolging van basen. (Eigenlijk zijn dit basenparen maar we hebben slechts één component van ieder paar nodig: C kan enkel voorkomen met G (en omgekeerd) en A kan enkel voorkomen met T (en omgekeerd)).
Er zijn vier verschillende basen: guanine, cytosine, adenine en thymine, afgekort met respectievelijk G, C, A en T. Hieronder vind je een voorbeeldstukje van een DNA-sequentie, voorgesteld in Python als een string:
"TACTTGTTGATATTGGATCGAACAAACTGGAGAACCAACATGCTCACGTCACTTTTAGTCCCT"
Bij het aanmaken van eiwitten in een organisme (bvb. bij het groeien van nagels), zijn er verschillende biochemische processen betrokken. Eén ervan is het proces dat men eiwitexpressie noemt. Tijdens dit proces wordt de DNA-sequentie van een gen vertaald in de zogenoemde aminozuursequentie van het eiwit. Dat gebeurt door telkens drie opeenvolgende basen te beschouwen. Zo’n basentriplet noemt men een codon. Er zijn dus in totaal \(4 \times 4 \times 4 = 64\) codons aangezien iedere base 4 mogelijke waarden kan aannemen. In de volgende tabel kan je opzoeken naar welk aminozuur een bepaald codon vertaald wordt. Er zijn slechts \(20\) aminozuren. Sommige aminozuren worden dus op basis van verschillende codons verkregen.
codon |
aminozuur |
codon |
aminozuur |
|
|---|---|---|---|---|
TTT |
F (Phenylalanine) |
TCT |
S (Serine) |
|
TTC |
F |
TCC |
S |
|
TTA |
L (Leucine) |
TCA |
S |
|
TTG |
L |
TCG |
S |
|
CTT |
L |
CCT |
P (Proline) |
|
CTC |
L |
CCC |
P |
|
CTA |
L |
CCA |
P |
|
CTG |
L |
CCG |
P |
|
ATT |
I (Isoleucine) |
ACT |
T (Threonine) |
|
ATC |
I |
ACC |
T |
|
ATA |
I |
ACA |
T |
|
ATG |
M (Methionine) |
ACG |
T |
|
GTT |
V (Valine) |
GCT |
A (Alanine) |
|
GTC |
V |
GCC |
A |
|
GTA |
V |
GCA |
A |
|
GTG |
V |
GCG |
A |
codon |
aminozuur |
codon |
aminozuur |
|
|---|---|---|---|---|
TAT |
Y (Tyrosine) |
TGT |
C (Cysteine) |
|
TAC |
Y |
TGC |
C |
|
TAA |
STOP |
TGA |
STOP |
|
TAG |
STOP |
TGG |
W (Tryptophan) |
|
CAT |
H (Histidine) |
CGT |
R (Arginine) |
|
CAC |
H |
CGC |
R |
|
CAA |
Q (Glutamine) |
CGA |
R |
|
CAG |
Q |
CGG |
R |
|
AAT |
N (Asparagine) |
AGT |
S |
|
AAC |
N |
AGC |
S |
|
AAA |
K (Lysine) |
AGA |
R |
|
AAG |
K |
AGG |
R |
|
GAT |
D (Aspartic acid) |
GGT |
G (Glycine) |
|
GAC |
D |
GGC |
G |
|
GAA |
E (Glutamic acid) |
GGA |
G |
|
GAG |
E |
GGG |
G |
Deze volgende code laat een functie aminoacid zien
die deze tabel in Python codeert. Gegeven een basentriplet (t.t.z. een
string van lengte 3) levert de functie een symbool terug dat staat voor
het overeenkomstige aminozuur. Later zullen we een techniek zien —
dictionaries — die ons zal toelaten om deze functie veel korter en
eleganter neer te schrijven. Momenteel gebruiken we gewoon een (zeer
lange) if constructie.
def aminoacid(triple):
if triple == "TTT" or triple =="TTC":
return "F"
elif triple in ("TTA","TTG","CTT","CTC","CTA","CTG"):
return "L"
elif triple in ("ATT","ATC","ATA"):
return "I"
elif triple == "ATG":
return "M"
elif triple in ("GTT","GTC","GTA","GTG"):
return "V"
elif triple in ("TCT","TCC","TCA","TCG","AGT","AGC"):
return "S"
elif triple in ("CCT","CCC","CCA","CCG"):
return "P"
elif triple in ("ACT","ACC","ACA","ACG"):
return "T"
elif triple in ("GCT","GCC","GCA","GCG"):
return "A"
elif triple in ("TAT","TAC"):
return "Y"
elif triple in ("TAA","TAG","TGA"):
return "STOP"
elif triple in ("CAT","CAC"):
return "H"
elif triple in ("AAT","AAC"):
return "Q"
elif triple in ("AAA","AAG"):
return "K"
elif triple in ("GAT","GAC"):
return "D"
elif triple in ("GAA","GAG"):
return "E"
elif triple in ("TGT","TGC"):
return "C"
elif triple == "TGG":
return "W"
elif triple in ("CGT","CGC","CGA","CGG","AGA","AGG"):
return "R"
elif triple in ("GGT","GGC","GGA","GGG"):
return "G"
else:
return None
Hieronder zien we een functie protein die, gegeven een DNA-sequentie,
de bijpassende aminozuursequentie oplevert. De functie vertrekt van een
variabele result die met de lege lijst geassocieerd wordt. Dan gaan we
de DNA-sequentie aflopen in slices van lengte \(3\), genomen van index \(i\)
tot \(i+3\). Deze index laten we in een for lus vertrekken vanaf \(0\) en
laten we in stappen van \(3\) verhogen. De variabele result wordt
telkens vervangen door de oude waarde van result geconcateneerd met
een singleton-lijst die uit het extra aminozuursymbool bestaat.
def protein(dna):
result = []
for i in range(0,len(dna),3):
result = result + [aminoacid(dna[i:i+3])]
return result
vb ="TACTTGTTGATATTGGATCGAACAAACTGGAGAACCAACATGCTC"
protein(vb)
['Y', 'L', 'L', 'I', 'L', 'D', 'R', 'T', 'Q', 'W', 'R', 'T', 'Q', 'M', 'L']
Ter vergelijking gebruikt volgende functie een list comprehension om dezelfde
eiwitexpressie te bereiken. We gebruiken een generator om alle indexen
i te genereren (met sprongen van 3) en gebruiken in de expressie van
de list comprehension deze index in een slice.
def protein2(dna):
return [ aminoacid(dna[i:i+3]) for i in range(0,len(dna),3) ]
protein2(vb)
['Y', 'L', 'L', 'I', 'L', 'D', 'R', 'T', 'Q', 'W', 'R', 'T', 'Q', 'M', 'L']
protein en protein2 doen beide precies hetzelfde maar werden
uitgewerkt m.b.v. een verschillende programmeerstijl. Dit noemt men 2
verschillende implementaties van hetzelfde probleem.
Gevalstudie 2: Simuleren van Populatiegroei¶
Stel dat we willen bestuderen hoe een populatie (bijvoorbeeld vissen in een vijver) zich gedraagt door de tijd heen. We zijn geïnteresseerd in hoe snel of hoe traag zo’n populatie groeit bij bepaalde omgevingsfactoren (bijvoorbeeld de hoeveelheid voedsel). Op het eerste zicht zou men denken dat populatiegroei te bestuderen valt met een eenvoudige meetkundige reeks: de populatie op tijdstip \(t+1\) is gewoon de populatie op tijdstip \(t\) vermenigvuldigd met een constante groeifactor. Maar dit gaat er van uit dat de groeimogelijkheid onbegrensd is; bijvoorbeeld dat voedselbronnen onuitputtelijk zijn. In de realiteit zijn deze bronnen begrensd en zal de populatie tijdens de groei een steeds groter wordende schaarste ondervinden en dus steeds langzamer groeien om uiteindelijk bij de maximale populatiegrootte te komen. Dit was het inzicht van de Belgische wiskundige Pierre-Francois Verhulst (1804-1849). Op basis van zijn analyse van bevolkingscijfers kwam Verhulst tot de conclusie dat de remming van de groei evenredig was met het verschil van de maximale populatie en de populatie op een gegeven tijdstip. Verhulst stelde daarom de volgende logistieke vergelijking op:
Deze vergelijking vertelt ons dus hoe de populatiegrootte \(P(t+1)\) op een bepaald tijdstip \(t+1\) tot stand komt op basis van de populatiegrootte op tijdstip \(t\) en gegeven een omgevingsfactor \(r\) (dat bijvoorbeeld model staat voor de hoeveelheid voedsel die voorhanden is). De populatiegrootte is in dit model een getal tussen \(0\) en \(1\): \(P(t) \in [0,1]\). 1 stelt de maximale grootte voor. Het is dus eigenlijk correcter om te spreken over populatiedichtheid.
Vervolgens kunnen we gaan bestuderen hoe deze groeivergelijking zich gedraagt door ze voor opeenvolgende tijdstippen uit te rekenen en dit rekenwerk bovendien voor allerlei keuzes van \(r\) te herhalen. We zullen bestuderen voor welke waarden van \(r\) dit leidt tot een stabiele populatie. Een stabiele populatie is een populatie die niet meer verandert eens bereikt, met andere woorden \(P(t+1) = P(t)\). Deze waarde \(x\) moet dus voldoen aan \(x = r.x.(1-x)\). Met andere woorden, het is het zogenoemde fixpunt van de functie \(f(x) = r.x.(1-x)\). Een fixpunt van een functie \(f\) is een waarde \(w\) zodat \(f(w)=w\).
Fixpunten berekenen¶
Fixpunten komen niet alleen in de studie van populaties aan bod. Het zijn regelmatig terugkerende objecten in de wiskunde. In de wiskunde is men er achter gekomen dat men fixpunten voor voldoende “gladde” functies (t.t.z. voldoend aantal keren continu differentieerbaar) kan berekenen door de functie herhaaldelijk toe te passen tot het resultaat convergeert. Dank zij onze kennis inzake iteratie kunnen we hiervoor nu Python gebruiken. Hieronder zien we een experiment dat het fixpunt van de cosinus benadert. We vertrekken van de beginwaarde \(0\) en berekenen dan 20 keer de cosinus van de vorige waarde:
import math
fix = 0
for i in range(0,20):
fix = math.cos(fix)
print (fix)
1.0
0.5403023058681398
0.8575532158463934
0.6542897904977791
0.7934803587425656
0.7013687736227565
0.7639596829006542
0.7221024250267079
0.7504177617637604
0.7314040424225099
0.7442373549005569
0.7356047404363473
0.7414250866101093
0.7375068905132427
0.7401473355678758
0.7383692041223231
0.7395672022122561
0.7387603198742112
0.739303892396906
0.7389377567153443
Indien we meer iteraties afwachten wordt het resultaat steeds preciezer en preciezer. De cosinus convergeert relatief snel naar zijn fixpunt maar dit hoeft niet altijd het geval te zijn. Sommige functies convergeren heel traag. De studie van de convergentiesnelheid en van het feit of er überhaupt convergentie optreedt is een zaak van de numerieke analyse. We gaan hier niet verder op in in deze cursus.
Experimenten met r¶
Laat ons nu terugkeren naar de logistieke functie \(f(x) = r.x.(1-x)\) en
bestuderen voor welke waarden van \(r\) er convergentie optreedt. Vermits we hebben gelezen dat
de logistieke functie relatief traag convergeert, gaan we de mogelijkheid
voorzien om het programma eerst een aantal keer “in het donker” te laten itereren alvorens
dan voor een gegeven aantal iteraties informatie op het scherm beginnen te printen.
Hieronder zien we een stuk
Python code dat eerst en vooral twee constanten introduceert om dit aantal iteraties vast te leggen.
Dan wordt de logistieke functie f definieert. De functie fixed_points tenslotte neemt
\(r\) als argument.
En dan wordt \(x = f(x)\) eerst een skip aantal keer berekend en daarna nog show aantal keer maar daarbij wordt de waarde van x telkens uitgeprint.
De beginwaarde is in deze implementatie 0.5. Deze beginwaarde voldoet voor de logistieke functie. Ook het kiezen van goede beginwaarden vormt studie van de numerieke analyse.
SKIP = 50
SHOW = 10
def f(x,r):
return r*x*(1-x)
def fixed_points(r):
x = 0.5
for itr in range(0,SKIP):
x = f(x,r)
for itr in range(0,SHOW):
x = f(x,r)
print (x)
Laat ons nu met fixed_points wat experimenteren om de stabiele
populatie voor verschillende waarden van \(r\) te onderzoeken. Hier is een
eerste experiment met \(r=3.2\).
fixed_points(3.2)
0.7994554904673701
0.5130445095326298
0.7994554904673701
0.5130445095326298
0.7994554904673701
0.5130445095326298
0.7994554904673701
0.5130445095326298
0.7994554904673701
0.5130445095326298
Dit is een overwacht resultaat! In plaats van te convergeren naar één fixpunt alterneert de logistieke functie tussen twee waarden! Een tweede experiment gebruikt \(r=3.5\). Het resultaat is nog raarder; de functie schijnt tussen \(4\) waarden te roteren.
fixed_points(3.5)
0.8269407065914387
0.5008842103072179
0.8749972636024641
0.38281968301732416
0.8269407065914387
0.5008842103072179
0.8749972636024641
0.38281968301732416
0.8269407065914387
0.5008842103072179
We kunnen ons nu afvragen of hier een algemen regel inzit, bijvoorbeeld: hoe groter \(r\) hoe meer fixpunten. Niets is minder waar. Uit de literatuur komt volgend overzicht:
\(0<r<1\) & de populatie sterft uit voor alle startwaarden
\(1<r<2\) & de populatie gaat naar (r-1)/r voor alle startwaarden
\(2<r<3\) & de populatie fluctueert een tijd maar gaat dan naar (r-1)/r voor alle startwaarden
\(3<r<3.45\) & de populatie oscilleert tussen 2 waarden voor bijna alle startwaarden
\(3.45<r<3.54\) & de populatie oscilleert tussen 4 waarden voor bijna alle startwaarden
\(3.54<r<3.57\) & de populatie oscilleert tussen 8, 16, 32, waarden voor bijna alle startwaarden
\(3.57<r<4\) & totale chaos, er is geen regelmaat meer en voor lichtjes verschillende startwaarden wordt heel verschillend gedrag waargenomen maar er zijn nog eilanden van regelmaat waar te nemen (bvb. rond 3.83 oscillatie tussen 3 waarden)
\(4<r\) & de waarden verlaten het interval \([0,1]\) en divergeren voor 32bijna alle startwaarden
Het Bifurcatiediagram¶
In plaats van de functie fixed_points telkens weer met de hand op te
roepen om te zien wat er gebeurt bij één bepaalde \(r\) kunnen
we de boel automatiseren en ook hiervoor Python gebruiken. In het
volgende programma bestuderen we het gedrag voor \(r\) waarden tussen \(=2.9\) en
\(4.0\). Er zitten oneindig veel getallen tussen die grenzen maar we beperken ons tot 100 getallen.
We doen dus 100 experimenten met 100 verschillende \(r\) waarden die op gelijke afstand van elkaar liggen in het interval \([2.9,4]\). Die lijst van \(r\) waarden is makkelijk te maken met een comprehension.
In elk experiment proberen we een fixpunt te benaderen zoals we deden in de
functie fixed_point hierboven. Opnieuw doen we eerst een aantal iteraties die we zelfs niet bekijken. Maar daarna gaan we de uitgerekende x waarden niet zomaar op het scherm afprinten maar ze verzamelen in een lijst.
Al de waarden in die lijsten gaan we t.o.v. de bijhorende \(r\) waarde afzetten in een scatter plot. In
een scatter zetten we functiewaarden uit maar mogen er per waarde op de
\(X-as\) meerdere waarden op de \(Y-as\) voorkomen. Wiskundig gesproken is
een scatter dus geen functie. We hebben deze eigenschap nodig in ons
experiment aangezien we juist willen bestuderen hoeveel fixpunten (hoeveel verschillende x waarden) er
bij iedere waarde van \(r\) horen.
Een scatter plot in de Matplotlib bibliotheek verwacht twee even lange invoerlijsten waar de elementen op de overeenkomstige posities een uit te zetten \(x-y\) koppel zijn.
Daarom wordt voor elke x waarde die in de loop wordt uitgerekend de bijhorende r waarde verzameld in
de lijst die de x_values van de plot gaan zijn en de x waarden zelf worden
verzameld in de lijst die de y_values van de plot gaan zijn.
import matplotlib.pyplot as plt
skip = 50
show = 10
nrpoints = 100
def f(x,r):
return r*x*(1-x)
def bifurcation(r0, rf):
rs = [r0 + (rf - r0)*i/(nrpoints - 1) for i in range(0,nrpoints)]
x_values = []
y_values = []
for r in rs:
x = 0.5
for itr in range(0,skip):
x = f(x,r)
for itr in range(0,show):
x = f(x,r)
x_values = x_values + [ r ]
y_values = y_values + [ x ]
return (x_values,y_values)
result = bifurcation(2.9, 4.0)
plt.scatter(result[0], result[1],1)
plt.show()

Het resultaat is verbluffend. Deze wereldberoemde figuur is het zogenoemde bifurcatiediagram. Dit diagram is een van de meest gekende visualisaties uit de tak van de wiskunde die chaostheorie heet. In deze subdiscipline onderzoekt men iteratieve systemen. Dat zijn systemen die bestaan uit recursievergelijkingen (zoals onze logistieke vergelijking) of uit differentiaalvergelijkingen waarvoor geen analytische oplossing bestaat en die men door herhaaldelijk herrekenen numeriek dient te benaderen.
Dikwijls zijn iteratieve systemen uiterst afhankelijk van de invoer. Een zeer minieme verandering van de invoer kan tot enorme veranderingen leiden in het gedrag van het systeem. Dat fenomeen wordt ook wel het butterfly effect genoemd: het flapperen van een vlindertje rond het vrijheidsbeeld van New York wordt na een tijdje door het aardse weersysteem opgeklopt tot de volgende tropische storm in de Caraïben. In het bifurcatiediagram zien we dat het aantal stabiele populaties en de waarden van de bijhorende populatiedichtheden uiterst afhankelijk zijn van \(r\). Zéér kleine veranderingen in de waarde van \(r\) geeft soms aanleiding tot enorm grote veranderingen in het aantal stabiele populaties. Natuurlijk bestond dit chaotisch gedrag ook al vóór er computers waren (het zijn ten slotte maar wiskundige vergelijkingen die men dikwijls genoeg dient te herhalen). Het is echter door de opkomst van de grafische mogelijkheden van computers dat men de systemen in zijn totaliteit heeft kunnen visualiseren. Met name de Frans-Poolse wiskundige Benoît Mandelbrot heeft hier bijzonder aan bijgedragen. Met het verschijnen van zijn “The Fractal Geometry of Nature”, toen hij in 1982 voor IBM werkte, werd chaostheorie populair bij wiskundigen en bij het grote publiek.
Samenvatting¶
In dit topic hebben we lijsten bestudeerd. We kunnen lijsten maken door
de elementen gewoon op te sommen, door een ingebouwde functie (zoals
range) te gebruiken of door de kracht van list comprehensions te
gebruiken. Lijsten verschillen van tupels doordat ze muteerbaar zijn.
Het verwerken van lijsten kunnen we doen door recursieve functies te
schrijven waarbij een indextellertje doorheen de recursie
getransporteerd wordt. Omdat dit echter vrij omslachtig is bestaat er
ook een for statement waarmee we zeer makkelijk alle elementen van een
lijst kunnen vastpakken om er een block code mee uit te voeren.
We hebben het topic afgesloten met twee gevalstudies die de kracht van lijsten en iteratie laten zien in de Biochemie en de Biologie. In het eerste voorbeeld kunnen DNA-strengen worden voorgesteld als lijsten en kan iteratie gebruikt worden om biochemische processen (zoals eiwitexpressie) mee te simuleren. In het tweede voorbeeld gebruiken we lijsten om alle gewenste waarden van \(r\) af te lopen en voor iedere waarde een lijst van fixpunten op te stellen. Deze lijsten worden dan overhandigd aan functies uit Matplotlib om plaatjes te maken.
