TOPIC 2: Basis Python¶

Dit is feitelijk het eerste hoofdstuk van de cursus. We starten met het bestuderen van de taal op interactieve wijze. In dit hoofdstuk beperken we ons tot de Python elementen die ons toelaten om de taal te gebruiken als een soort van veredelde rekenmachine.

De allereerste programma’s die we voorstellen kunnen dan ook niet veel meer dan wat we reeds met een wetenschappelijke rekenmachine kunnen. Toch is deze stap belangrijk aangezien we hierdoor een aantal Python concepten zullen bijbrengen die vanaf het volgende hoofdstuk wel cruciaal zullen zijn om de rest van de taal te begrijpen.

Naar het einde van dit hoofdstuk toe laten we zien hoe (stukken) programma’s geschreven door derden gebruikt kunnen worden zonder dat we zelf daarvoor reeds geavanceerde Python dienen te kennen. Zulke stukken programma’s die we kunnen gebruiken zonder noodzakelijk te moeten programmeren worden doorgaans “bibliotheken” genoemd. Wij zullen dit illustreren aan de hand van een Python bibliotheek waarmee men grafieken van meetwaarden kan uitzetten. Hiermee tonen we meteen vanaf het begin het nut aan van Python voor wetenschappers en ingenieurs.

De Read-Eval-Print Lus¶

Een codecel zoals je er doorheen de notebooks ziet kan je gebruiken als een Read-Eval-Print lus. De read-eval-print-lus bestaat uit drie fasen:

Read¶

Van zodra je een fragment code dat je hebt ingetypt in een codecel probeert te runnen zal Python — lettertje per lettertje — analyseren wat je hebt ingevoerd. Python probeert dus te lezen wat je hebt ingetypt. Python zal enkel doorgaan met de volgende fase van zodra hij er in geslaagd is jouw invoer te ontcijferen. Hiertoe dient wat je invoert de schrijfregels van Python te respecteren. Net zoals bij natuurlijke taal, heeft een programmeertaal bepaalde schrijfregels en een grammatica. Deze noemt met de syntax van de programmeertaal. De syntax van de taal schrijft voor welke letterreeksen wél en geen geldige Python zijn. Indien de read fase ontdekt dat jouw invoer geen geldige Python is, zal ze klagen met een foutmelding. We spreken in dit geval over een syntaxfout. Probeer eerst de volgende codecel die correcte Python bevat en daarna eens de codecel die er op volgt die foute Ptyhon bevat. Bij de eerste cel wordt niet geklaagd, integendeel zoals hier vlak na wordt uitgelegd krijg je het resultaat te zien van de uitvoer van het codefragment in de cel. Maar bij de tweede cel wordt een syntax fout aangeduid. Die laatste haak staat daar niet op zijn plaats.

(8 + 2) / 2.0   

5.0

(8 + 2) / 2.0) 

  File "<ipython-input-2-e5cb8cd1bde8>", line 1
    (8 + 2) / 2.0)
                 ^
SyntaxError: invalid syntax

Eval¶

Eens Python erin geslaagd is van je invoer te controleren op spelfouten en grammaticale fouten, zal hij overgaan tot de evaluatiefase. In deze fase wordt je invoer daadwerkelijk omgezet in actie. In ons voorbeeld zal Python de opteling en deling effectief uitvoeren. De evalfase is dus de eigenlijke rekenfase. Na de evalfase zal het resultaat ergens in het computergeheugen opgeslagen zitten. Het is pas de volgende printfase die het resultaat op het scherm zal laten zien. Ook tijdens het rekenen kan er vanalles mislopen. Met de volgende codecel kan je bijvoorbeeld zien wat er gebeurt als je 1/0 intikt. Alhoewel deze uitdrukking de schrijfregels van Python respecteert (“Iedere deling moet links en rechts een operand hebben”) en dus de readfase zal overleven, zal de evalfase tot de constatering komen dat er iets mis is. Dit gebeurt tijdens het rekenen. In dit geval spreken we van een semantische fout of ook wel runtime fout. De semantiek van een programmeertaal schrijft voor wat de betekenis is van een uitdrukking. Een semantische fout is dus een fout die ingaat tegen de betekenis van de taal. In ons geval is het een fout die de betekenis van het deelteken niet respecteert. Je krijgt dan een “division by zero” fout. De rest van de foutmelding zullen we later bestuderen.

1 / 0

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-3-bc757c3fda29> in <module>
----> 1 1 / 0

ZeroDivisionError: division by zero

Print¶

De printfase schiet pas in actie als zowel de readfase als de evalfase zonder foutmeldingen werden afgerond. Python zal het resultaat dan netjes afdrukken vlak onder de codecel.

Whitespace¶

De leesfase is vrij tolerant voor wat betreft het gebruikt van whitespace, i.e. spaties bij het schrijven van een expressie. We zullen later zien dat Python een vrij specifiek gebruik heeft van whitespace om blokken code af te lijnen maar voorlopig is het voldoende om naar onderstaande experimentjes te kijken om te zien dat een spatie meer of minder in een expressie er niet toe doet. Er natuurlijk wel een verschil tussen 24 en 2 4. Het eerste is het getal vierentwintig, het tweede zijn 2 getallen nml 2 en 4.

(8 + 2) / 2

5.0

(8+2)/2   

5.0

( 8 + 2 ) / 2   

5.0

Python Expressies, Waarden en Types¶

De stukjes geldige tekst die je intikt in een codecel noemt men expressies of uitdrukkingen. Een uitdrukking wordt na het correct lezen geëvalueerd door de evalfase. Het resultaat hiervan is een waarde. Sommige uitdrukkingen zijn zo eenvoudig dat ze meteen gelijk zijn aan hun waarde. Neem bijvoorbeeld de uitdrukking 3. Deze is triviaal geldige Python. De evaluatie ervan zal aanleiding geven tot de waarde 3. Deze waarde wordt meteen ook geprint als 3. Men zegt dat getallen “gewoon naar zichzelf evalueren”.

De meeste uitdrukkingen evalueren echter niet naar zichzelf. Neem bijvoorbeeld 1+3. Dit is een geldige Python uitdrukking en zal dus de readfase overleven. De evalfase zal de uitdrukking evalueren naar het getal 4 en de printfase zal 4 afdrukken op het scherm. Men zegt dat 4 de waarde is van de uitdrukking 1+3.

1+3

Een interactieve sessie met Python er dus op neer dat je heel de tijd in de read-eval-print-lus expressies invoert. Python controleert je expressie op schrijffouten en evalueert de expressie naar een waarde. De printfase drukt de waarde op het scherm af. Syntaxfouten zijn fouten die gevonden worden in de readfase. Runtime fouten zijn fouten die gevonden worden tijdens de evaluatiefase.

Types¶

Uit de wiskunde weet je al dat waarden tot verschillende verzamelingen behoren. Zo is \(3 \in \mathbb{N}\) maar \(3,14 \notin \mathbb{N}\) maar echter wel \(3,14 \in \mathbb{R}\). In Python zeggen we dat “3 van het type int is” en dat “3.14 van het type float is”. Merk op dat Python (en de meeste programmeertalen) een puntje gebruiken om een decimale getal te noteren en niet de komma die je uit de basisschool gewend bent.

int staat voor “integer number” (wat zoveel als “geheel getal” betekent in het Engels) en float staat voor “floating point number”. Dat laatste slaat op de manier waarop reële getallen in de computerhardware worden voorgesteld. De technische details hiervan vallen helaas buiten het bestek van dit boek.

Merk op dat een waarde slechts tot één enkel type kan behoren. In de wiskunde is zowel \(3 \in \mathbb{N}\) als \(3 \in \mathbb{R}\) waar. In Python is 3 wel van het type int maar niet van het type float. Indien we het reëel getal \(3\) bedoelen dienen we uitdrukkelijk 3.0 te schrijven. In principe hebben 3 en 3.0 niks met mekaar te maken. Deze kieskeurigheid van Python is een bron van vele fouten bij beginnende Python programmeurs.

In de wiskunde is het belangrijk te weten in welke verzameling men aan het werken is. Zo zal de functie \(log\) volledig gedefinieerd zijn indien we erbij vertellen dat de verzameling waarbinnen we werken \(\mathbb{R}^+_0\) is. \(log\) is echter deels ongedefinieerd indien we zeggen dat \(log : \mathbb{R} \rightarrow \mathbb{R}\) aangezien \(log\) geen zin heeft voor nul en voor negatieve getallen. Dat laatste is dan weer geen correcte uitspraak indien we erbij vertellen dat de verzameling van het resultaat van de functie \(\mathbb{C}\) is.

Python (en vele andere programmeertalen) gaan voor de verschillende operatoren die ze ondersteunen ook type informatie gebruiken. Indien we bijvoorbeeld twee int getallen meegeven aan de operator + zal hij een resultaat van type int opleveren. Indien één van beide getallen echter van het type float is, zal de operator een resultaat van het type float teruggeven. Dit wordt geïllustreerd door de volgende reeks codecellen:

17 + 10

17.0 + 10.0 

27.0

17.0 + 10

27.0

17 + 10.0

27.0

17 + 10.   

27.0

17. + 10

27.0

Je kan in Python expliciet zelf type conversie doen. Zo kan je een int getal dwingen om zich om te vormen naar een float getal zoals in onderstaande codecel.

float(3)

3.0

Wat een operator juist doet kan van taal tot taal verschillen en zelfs van de ene versie van de taal naar de andere. Voor de deling bijvoorbeeld bestaat in Python 3.0 een standaard deling /. De deling van 2 int getallen zal een resultaat van type float opleveren. Maar er bestaat ook een //. Dat is een deling die naar beneden afrondt (in het Engels floor). Die zal bij de deling van 2 int getallen een resultaat van type int opleveren. Maar als ten minste één van de de argumenten van type float is krijg je een float als antwoord maar die is nog altijd naar beneden afgerond.

16 / 2

8.0

17 / 2

8.5

17 // 2

17 // 2.0

8.0

Reele vs. `float` getallen¶

Hierboven hebben we geïnsinueerd dat het type float overeenkomt met de verzameling \(\mathbb{R}\). Dat is echter niet correct. Intuïtief kan je al aanvoelen dat er slechts een eindig aantal getallen bestaat van het type float. Dat komt simpelweg omdat een computer een eindige machine is met een eindige hoeveelheid geheugen. Het type float is dus slechts een deelverzameling van \(\mathbb{R}\). Irrationele getallen zoals \(\pi\) kunnen we alvast niet voorstellen in zo’n machine. Voor zulke getallen werk men met een benadering met een eindige precisie. Onderstaande codecellen illustreren dit. Er gebeuren duidelijk afrondfouten tijdens het uitvoeren van berekeningen. Het is dus opletten geblazen wanneer je continue wiskunde gaat beoefenen met een computer! Binnen de computerwetenschappen is er een hele nieuwe tak van de wiskunde ontstaan die onderzoekt hoe je continue wiskunde correct kan benaderen m.b.v. eindige float getallen. Deze subdiscipline heet de numerieke analyse en vormt het onderwerp van een gelijknamig keuzevak in de hogere jaren.

1.0 / 3.0

0.3333333333333333

1.0 / 3.0 + 1.0 / 3.0 

0.6666666666666666

1.0 / 3.0 + 1.0 / 3.0 + 1.0 / 3.0

1.0

Complexe Getallen¶

Naast (benaderingen van) reële getallen kent Python ook (benaderingen van) complexe getallen. Dit zijn waarden van het type complex. Hier zien we al dat Python in vele opzichten meer dan andere programmeertalen geschikt is voor wetenschappers en ingenieurs. Het type complex zit in de meeste programmeertalen niet ingebouwd. Hieronder zien we enkele experimenten die ons toelaten van het type beter te begrijpen.

12j

12j

4+8j

(4+8j)

1j * 1j

(-1+0j)

In tegenstelling tot de wiskunde spreken we in Python van \(j^2=-1\) in plaats van de meer traditionele notatie \(i^2=-1\). De keuze voor de letter \(j\) is een traditie die veelal door Amerikaanse ingenieurs wordt gevolgd. Het Python getal 12j komt dus strikt genomen overeen met wat wij zouden opschrijven als \(0+12i\) oftewel \(12i\). Het derde experimentje laat duidelijk zien dat \(j^2=-1\).

Het is wel belangrijk om j te onderscheiden van 1j. Het laatste is wat wij kennen als het complexe getal \(i\). Het eerste is een gewone variabelennaam (net als ‘x’ in de wiskunde). Intypen van gewoon j resulteert dus in een foutmelding. Python klaagt dat hij die variabelennaam (nog) niet kent. We zullen in een latere sectie variabelen bestuderen.

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-26-3eedd8854d1e> in <module>
----> 1 j

NameError: name 'j' is not defined

Strings¶

We kennen nu reeds de types int, float en complex. We voeren nu nog snel een vierde type in alvorens we met wat interessantere dingen van start kunnen gaan: het type str wat staat voor “string”.

"Hallo"

'Hallo'

Strings (of in loepzuiver Nederlands ook wel strengen genoemd) zijn reeksen van karakters. Ieder karakter komt grofweg overeen met een letter of symbool dat je op je toetsenbord kan vormen. De karakters van een streng worden gegroepeerd tussen enkele of dubbele quotes. Je mag dus ’hallo’ of "hallo" schrijven maar niet "hallo’ of ’hallo".

Strings worden door de evaluator letterlijk genomen en worden dus nooit in vraag gesteld: een string evalueert naar zichzelf en wordt niet verder geanalyseerd. Het maakt dus niet uit of de string correct Engels, Nederlands of wat dan ook is. Ook "hkd@fKsj123.. ..12;" is een correct gevormde string:

"hkd@fKsj123..  ..12;"

'hkd@fKsj123..  ..12;'

In tegenstelling tot wat je misschien zou verwachten, zijn er toch een aantal betekenisvolle operatoren toepasbaar op strings. De meest nuttige is de operator + die twee stringwaarden aan elkaar plakt. Dit wordt de concatenatie-operator genoemd. Hieronder zien we hem aan het werk:

"Frank" + "en" + "stein"

'Frankenstein'

Het “optellen” van strings is dus niets anders dan het aaneenplakken van de operanden. Het is belangrijk het verschil tussen strings en getallen te begrijpen bij het gebruik van +. Hieronder zien we duidelijk dat + getallen optelt maar strings concateneert:

3 + 3 + 3

'3' + "3" + "3"

'333'

Iha noemt men een operator zoals de + die een andere betekenis krijgt naargelang de types van de argumenten waarop hij wordt toegepast overladen (Engels: overloaded).

Wat zou er gebeuren indien we + gebruiken met strings en getallen door mekaar gemengd? Probeer het uit!

3 + "Hallo"

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-32-b8c7fb6dd4d3> in <module>
----> 1 3 + "Hallo"

TypeError: unsupported operand type(s) for +: 'int' and 'str'

Maar grappig genoeg zal de * wel werken als je een integer en een string probeert te vermenigvuldigen:

7 * "ho"

'hohohohohohoho'

Samenvatting¶

We hebben in deze sectie besproken wat expressies en hun waarden zijn. Expressies zijn stukken tekst die aan de Python syntaxregels voldoen. Waarden ontstaan na evaluatie van een expressie. Iedere waarde heeft een type. We hebben tot nu toe \(4\) types besproken. De types zijn niet alleen een leuke naam voor een verzameling waarden. Ze bepalen ook welke operatoren er toepasbaar zijn op die waarden. Sommige operatoren zijn wél toepasbaar op sommige types en niet toepasbaar op andere. Sommige operatoren hebben een verschillende betekenis indien we ze toepassen op waarden van verschillende types. Zulke operatoren noemen we overladen.

Functies en Operators¶

Een krachtig werktuig uit de wiskunde zijn functies. Deze “doen” iets indien we ze toepassen op een bepaalde waarde. Zo berekent de functie \(sin\) de sinus van een gegeven reëel getal. Het mag dan ook niet verwonderen dat functies (naast operatoren) één van de basiswerktuigen vormen van de (Python) programmeur.

Zowel functies als operatoren worden toegepast op een of meerdere waarden en leveren één resultaatwaarde op. sin wordt bijvoorbeeld toegepast op één waarde. + wordt toegepast op twee waarden. Beide leveren uiteraard één resultaatwaarde op. De waarden waarop we ze toepassen worden de argumenten genoemd. In het geval van operatoren spreken we ook wel over operanden.

Ingebouwde Functies Oproepen¶

Python kent een aantal functies die gewoon in de taal zijn ingebouwd. Een voorbeeld hiervan is de abs functie die de absolute waarde van een getal teruggeeft. Hier zien we ze aan het werk:

abs(-9)

abs(9)

abs(-9) is dus de Python-notatie voor wat we in de wiskunde als \(|-9|\) zouden schrijven. In Python zeggen we dat een functie een naam heeft (hier: abs) en wordt toegepast, opgeroepen of aangeroepen met het juiste aantal argumenten. In het geval van abs is er slechts één argument maar dat hoeft niet altijd het geval te zijn. Hieronder zien we de functie pow aan het werk. Deze neemt twee argumenten en verheft het eerste argument tot de macht aangeduid door het tweede argument. Bemerk dat de argumenten van zo’n functie door komma’s worden gescheiden. Dit laatste is één van de syntaxregels van Python.

pow(2,3)

pow(2.5,1.0/3.0)

1.3572088082974532

Deze stukjes Python-code berekenen dus respectievelijk \(2^3\) en \(\sqrt[3]{2.5}\).

Zoals reeds gezegd bestaat er een sterk verband tussen functies en operatoren. Soms kent Python zelfs hetzelfde concept, zowel als operator als als functie. Dat is het geval voor de machtsverheffing. Naast bovenstaande oproep als functie kunnen we deze ook verkrijgen door toepassing van de operator **. Het onderstaande is dus volledig equivalent met het voorgaande experimentje.

2**3

2.5**(1.0/3.0)

1.3572088082974532

Voorrangsregels op Operatoren¶

Het laatste experiment toont aan dat we — net als in de wiskunde — soms haakjes dienen te gebruiken als we verschillende operatoren beginnen te mengen in éénzelfde uitdrukking. Hieronder zien we nog enkele experimentjes die dat tonen:

212 - 32.0 * 5.0 / 9.0

194.22222222222223

212 - ((32.0 * 5.0) / 9.0)

194.22222222222223

(212 - 32.0) * 5.0 / 9.0

100.0

In de eerste expressie worden aftrekking, vermenigvuldiging en deling tesamen gebruikt in één expressie. Zoals we verwachten worden vermenigvuldiging en deling uitgerekend vóór de aftrekking. Er gelden dus voorrangsregels tussen de operatoren. In het algemeen volgen deze regels de volgorde die je uit de wiskunde gewend bent. Dit wordt geïllustreerd in de tweede expressie. De derde expressie toont aan dat we haakjes dienen te gebruiken indien we deze automatisch toegepaste voorrangsregels willen uitschakelen. De voorrangsregels zijn: eerst **, dan *, /, % en pas dan +, -

Ingebouwde Functies en Operatoren¶

Men kan zich nu de vraag stellen wat de volledige lijst van functies en operatoren is die Python kent. Het is geenszins de bedoeling dat je deze lijst gaat opzoeken en vanbuiten leren. Gaandeweg zal je de meest gebruikte functies en operatoren van buiten kennen gewoon door ze veel te gebruiken tijdens je programmeerwerk. Voor de minder frequent gebruikte kan je online op python.org alle nodige informatie vinden. Let wel dat je de juiste versie van Python bekijkt: in deze cursus gebruiken we Python 3.

De laatste experimenten laten ten slotte de functie type aan het werk zien. Dit is een (niet-wiskundige) functie die het type van een waarde weergeeft. Zo laten we zien dat \(3\) van het type int is, dat 3.8 van het type float is, en dat \(12+12i\) van het type complex is. Zeer interessant is dat ook “waarden” als abs een type hebben. Volgens Python is het type van abs een ingebouwde functie. De meer filosofisch geïnspireerde student kan proberen na te denken wat type(int) of zelfs type(type) zou opleveren. Probeer het uit!

type(3)

int

type(3.8)

float

type(12+12j)

complex

type("Hallo")

str

type(abs)

builtin_function_or_method

type(int)

type

type(type)

type

Variabelen¶

Tot hiertoe hebben we Python eigenlijk slechts als eenvoudige rekenmachine gebruikt. Vanaf deze sectie schakelen we een versnelling hoger en beginnen we met het gebruiken van de volledige kracht van de computer. In dit en de komende hoofdstukken zullen we geleidelijk aan de verschillende taalonderdelen van Python invoeren. Python zal aldus steeds krachtiger en krachtiger worden om wetenschappelijke problemen uit te rekenen of om bijvoorbeeld een heus computerspel te bouwen. We beginnen met variabelen.

De Toekenning¶

In de wiskunde worden variabelen (zoals \(x\)) gebruikt om onbekenden aan te duiden. In de computerwetenschappen is dit eigenlijk net andersom: variabelen zijn namen die staan voor bekende waarden. Beschouw bijvoorbeeld volgende interactie:

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
<ipython-input-50-6fcf9dfbd479> in <module>
----> 1 x

NameError: name 'x' is not defined

Python klaagt dat x een ongedefinieerde naam is. In de volgende codecel zien we een nieuw Python element: een = teken met links een naam en rechts een willekeurige expressie. Dit noemen we een toekenning of assignment in het Engels. Een toekenning beveelt Python de naam toe te voegen aan zijn intern geheugen en die naam te associëren met de waarde van de expressie. Dat is \(10\) in ons geval. Vanaf nu is x wél gedefinieerd en levert het evalueren van x de geassocieerde waarde op. We kunnen vanaf nu x gebruiken zoals gelijk welk andere expressie. We kunnen x dus gebruiken als deel van een samengestelde expressie, als argument van een functie aanroep en zelfs als rechterkant van een andere toekenning.

x=8+2

x*5

pow(x,3)

y=x+1

Statements¶

Indien we even terugkijken naar de lijn waar we x gedefinieerd hebben, observeren we een nieuw fenomeen: na het intypen van x=8+2 print de REPL geen waarde op het scherm af. We kunnen dus stellen dat x=8+2 geen expressie is aangezien we eerder hadden afgesproken dat elke expressie een waarde heeft die door de REPL wordt afgeprint.

Het taalelement x=8+2 is het eerste voorbeeld van wat we een statement noemen. Statements zijn commando’s die we aan de computer geven zonder dat we daar een waarde van verwachten. Met het statement x=8+2 bevelen we Python als het ware om de variabele x in het geheugen vanaf nu te associëren met de waarde 10. Het uitvoeren van dat bevel levert geen waarde op die kan geprint worden door de REPL. De toekenning is slechts het eerste voorbeeld van de vele soorten statements die we vanaf nu zullen tegenkomen.

Toekenning (vervolg)¶

We kunnen ons nu de vraag stellen wat er gebeurt indien de naam van een toekenning reeds in het geheugen zit. Het antwoord is eenvoudig: de oude waarde waarmee de naam geassocieerd is wordt gewoon vergeten en vervangen door de nieuwe waarde. Bekijk hetvolgende experiment:

x=10

y=x*20

x=30

We zien hier dat x gedefinieerd wordt en geassocieerd wordt met de waarde \(10\). Dan wordt y gedefinieerd op basis van x en meteen daarna wordt x opnieuw gedefinieerd en geassocieerd met \(30\). Maar er bestaat maar één x in het Python geheugen. Deze is vanaf nu verbonden met de waarde \(30\) en de originele waarde wordt “vergeten” door Python.

Merk op dat waarden die berekend werden op basis van de oude waarde van x niet automatisch heruitgerekend worden. Dit zien we als we y evalueren ná het herdefiniëren van x.

Het feit dat variabelen zowel links als rechts van het = teken mogen voorkomen levert ons natuurlijk de vraag op wat er gebeurt indien dezelfde variabele zowel links als rechts van dat teken staat. Wat gebeurt er bijvoorbeeld als we x = x + 1 evalueren? Het antwoord zien we hieronder:

x=10

x=x+1

Wat er exact gebeurt bij het uitvoeren van een statement van de vorm variabele = expressie is het volgende: eerst wordt de expressie uitgerekend (gebruik makend van de oude waarde van de variabele dus) en pas nadien wordt de variabele geassocieerd met de nieuwe waarde. Het statement x = x + 1 gaat de waarde van x dus vervangen door de oude waarde van x, verhoogd met \(1\). Dit is niet zomaar een theoretische snuisterij. Het wordt zeer veel gebruikt bij het programmeren in Python. Hieronder zien we hoe we kunnen berekenen hoe een kapitaal van \(300\) Euro groeit (m.b.v. enkelvoudige interestberekening) door het \(37\) jaar op de bank te zetten aan \(4\) percent.

kapitaal = 300

kapitaal = kapitaal + (kapitaal * 4.0 * 37)/100

kapitaal

744.0

Rest ons nog uit te leggen dat er verscheidene varianten bestaan van de toekenning. Naast = bestaan ook nog +=, -=, *=, /=, enz… . Dit zijn afkortingen die door sommigen graag gebruikt worden. Zo staat x += exp bijvoorbeeld voor x = x + exp. De auteurs van dit boek vinden dat de afkorting veel minder makkelijk leest dan het origineel. Wegens de populariteit van de afkortingen is de kans echter groot dat je dit soort statements tóch tegenkomt indien je andermans code dient te lezen.

Hieronder zien we één voorbeeldje van het gebruik van zo’n afgekort assignment statement. Het statement x *= 5 is dus volledig equivalent aan x = x * 5.

x = 10

x *= 5

Constanten¶

Stel dat we Python gebruiken om ons te helpen bij het oplossen van meetkunde vraagstukken waarbij we dikwijls de waarde van pi nodig hebben tot op een grote precisie. Je kan beslissen on telkens een lange rij cijfers te typen maar het is beter om pi als een variabele in te voeren. De kans dat je je vergist bij het intikken van de naam pi is veel kleiner dan de kans dat je ergens een cijfer verkeerd tikt. Bovendien zal Python je zelfs waarschuwen als je een tikfout maakt in de naam pi. Zolang je de variable pi dan gerust laat dient ze als een constante.

pi = 3.141592653589

Modules¶

Python komt met een heleboel ingebouwde functies. We leren later ook hoe we zelf nieuwe functies kunnen definiëren. Maar er zijn ondertussen al een hele hoop bibliotheken of modules beschikbaar die constanten en functies bevatten die door andere programmeurs ontwikkeld zijn. Je kan die modules inladen en gebruiken. Je kan als het ware het werk van die andere programmeurs gaan hergebruiken waardoor je zelf sneller een interressant programma kan schrijven.

Later gaan we ook zien hoe we code die we zelf ontwikkeld hebben kunnen opdelen en wegschrijven in verschillende files om ze daarna te hergebruiken. Modularisatie is een heel krachtige techniek in programmeren en laat toe om de complexiteit van heel grote programma’s te gaan beheersen. Maar hier gaan we in eerste instantie laten zien hoe je een bibliotheek die met Python is meegeleverd kan aanspreken. Dat wordt hieronder geïllustreerd met math en cmath. De eerste bevat heel wat nuttige spullen om reële wiskunde te bedrijven. De tweede bevat voor heel veel van die dingen de variante voor complexe getallen.

Een module importeren¶

Met het import statement kunnen tegen de REPL zeggen welke modules we allemaal nodig zullen hebben. Hieronder laten we zien hoe dat werkt. We importeren de math module. Die zit boordevol nuttige wiskundige dingen. Dat zijn variabelen zoals bijvoorbeeld pi, maar ook functies zoals bijvoorbeeld sin, cos en sqrt die de vierkantswortel van een getal berekent (Eng: square root). Je moet die nu echter aanpreken met respectievelijk math.pi, math.sin, math.cos en math.sqrt.

import math

math.pi

3.141592653589793

math.cos(12)

0.8438539587324921

math.sqrt(16.0)

4.0

Op het eerste zicht lijkt het wat onhandig dat we vóór iedere naam die we wensen te gebruiken (t.t.z. pi, cos en sqrt) “handmatig” math. moeten plakken. Maar er zijn een aantal belangrijke voordelen. Een eerste voordeel is dat er geen botsingen kunnen zijn tussen de namen van de functies en variabelen in je eigen code en die in een willekeurige module die je importeerde. Een ander voordeel aan het handmatig “vastpakken” van een functie of variabele uit een module, is dat er twee totáál verschillende modules kunnen bestaan die identieke variabelen en functies bevatten maar met een geheel andere betekenis. Dat laten we hieronder zien.

Zowel math als cmath zijn modules die met Python zijn meegeleverd. De eerste bevat heel wat nuttige spullen om reële wiskunde te bedrijven. De tweede bevat voor heel veel van die dingen de variante voor complexe getallen. Beschouw volgende experimenten.

We beginnen met zowel de modules math als cmath te importeren in de REPL. Dan zien we dat beide modules een identieke naam pi bevatten die geassocieerd is met dezelfde waarde.

import math
import cmath

math.pi

3.141592653589793

cmath.pi

3.141592653589793

Nadien wordt het interessant. Eerst gebruiken we math om de vierkantswortel van \(-1\) te berekenen wat zoals verwacht een foutmelding oplevert. Indien we hetzelfde doen met de versie van sqrt in cmath, dan zien we dat we netjes het verwachte resultaat \(1j\) krijgen.

math.sqrt(-1)

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
<ipython-input-81-2037b8d41d70> in <module>
----> 1 math.sqrt(-1)

ValueError: math domain error

cmath.sqrt(-1)

1j

Een tweede voorbeeld is de exp functie die ook door beide modules wordt aangeboden. In het geval van math berekent deze \(e^r\) voor een reëel getal \(r\). In het geval van cmath berekent ze \(e^{a+bi}\) voor een willekeurig complex getal \(a+bi\). De exp functie uit de math bibliotheek zal zoals verwacht niet werken op een complex getal waar de exp functie uit de cmath bibliotheek dat wel aankan.

math.exp(1)

2.718281828459045

cmath.exp(1)

(2.718281828459045+0j)

math.exp(1+2j)

---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-85-1a2ef427e363> in <module>
----> 1 math.exp(1+2j)

TypeError: can't convert complex to float

cmath.exp(1+2j)

(-1.1312043837568135+2.4717266720048188j)

Een andere naam kiezen voor een module¶

Soms is het gewenst een module te importeren onder een andere naam dan de naam die door de makers van de module bedacht werd. Stel dat we de modules math en cmath zouden willen importeren onder de namen wiskunde en complexe_wiskunde. Dit is mogelijk dank zij het import ... as ... statement. Hier zien we dit statement aan het werk:

import math as wiskunde
import cmath as complexe_wiskunde

complexe_wiskunde.sqrt(-1)

1j

wiskunde.cos(12)

0.8438539587324921

Merk op dat het import ... as ... de naam van de module niet verandert op je harde schijf of in de cloud. Al wat we doen is als gebruiker van een module “lokaal” (t.t.z. enkel in onze REPL) een andere naam gebruiken dan de eigenlijke naam van de module. We zouden dit bijvoorbeeld kunnen doen omdat we van oordeel zijn dat de makers van een module niet zo’n veelzeggende naam gekozen hebben of omdat de naam te lang is om veel in te tikken.

De inhoud van een module importeren¶

Er is een verschil tussen het importeren van een module in zijn geheel (wat we tot nu toe gedaan hebben) en het importeren van de inhoud van een module. Dat laatste kunnen we doen m.b.v. het from ... import ... statement. Bijvoorbeeld kunnen we beslissen om alles uit de module math te importeren door from ... import * te gebruiken (het sterretje staat dus voor “alles”):

from math import *

sqrt(4)

2.0

cos(pi)

-1.0

Python heeft als het ware de hele module math beschouwd en één voor één alle variabelen en functies “gekopieerd” naar de REPL. Het grote voordeel is dat we nu de modulenaam met de puntjessyntax niet meer hoeven te gebruiken. Dat schrijft dus makkelijker. Het nadeel is dat het niet meer mogelijk is om twee verschillende modules te gebruiken die variabelen en functies met dezelfde namen bevatten. Bij het importeren van de inhoud van de tweede module zou deze in de REPL alles overschrijven wat we uit de eerste module geïmporteert hadden. Het is precies dank zij de notatie met het puntje dat we twee modules als math en cmath tegelijk kunnen gebruiken zonder dat dezelfde namen van variabelen en functies uit beide modules mekaar voor de voeten lopen; het zijn immers wij als gebruikers die “met de hand” (correcter: met de punt) zeggen welke functie uit beide modules we precies bedoelen.

Een alternatief is om een expliciete lijst op te sommen van de dingen die we willen importeren. Dan worden alleen de opgesomde variabelen en functies “gekopieerd” naar de REPL. Bijvoorbeeld:

from math import cos, sin

cos(pi)

-1.0

Zelf een module maken (en importeren)¶

Je kan ook zelf een stuk code schrijven en naar een file wegschrijven die je dan later als een module kan importeren. Dat kan je doen door

een nieuw notebook aan te maken (selecteer ‘New Notebook’ in ‘File’ menu),
daar je code in te schrijven,
een naam voor je file te kiezen (selecteer ‘Rename’ in ‘File’ menu)
en dan die file te downloaden naar je computer als een .py file (selecteer ‘Download as’ ‘Python (.py)’ in ‘File’ menu).

Daarna moet je die file dan in dezelfde folder slepen als waar het notebook instaat waarin je de code als module wil importeren.

Omdat we nog niet veel Python kennen testen we voor deze cursusnota’s met een zeer klein voorbeeld. We maken een nieuw notebook en in een codecel introduceren we twee variabelen: lengte = 1.80 en gewicht = 85 (je mag gerust je eigen data als voorbeeld invoeren). We geven de file de naam mijn_data en downloaden de file als een .py file. Die file plaatsen we in dezelfde folder als dit notebook.

In onderstaande codecel importeren we dan ons zelfgeschreven programma (van 2 lijnen) en berekenen onze BMI (Body Mass Index).

import mijn_data
mijn_data.gewicht / mijn_data.lengte ** 2

24.337479718766904

Samenvatting¶

We hebben in deze sectie gezien hoe we en bestaande modules kunnen inladen en gebruiken. We hebben drie varianten van het import statement gezien:

De eerste twee importeren een module. De laatste importeert de inhoud van een module.

We weten nu ook hoe we code die we zelf schrijven kunnen wegschrijven op een file die we later als een module kunnen importeren.

We hebben tot nu toe nogal wat Python constructies gezien. Het is onze bedoeling om zo snel mogelijk “iets echts” te doen met Python; t.t.z. iets dat het nut aantoont van Python voor wetenschappers en ingenieurs. Dat is het onderwerp van sectie 1.7{reference-type=”ref” reference=”sec:matplotlib”} waar we de matplotlib bibliotheek zullen gebruiken om wetenschappelijke grafieken te tekenen. Daarvoor hebben we eerst echter nog één nieuwe soort Python waarden (t.t.z. een nieuw type) nodig, namelijk tupels.

Tupels¶

Tupels zijn in de wiskunde bekend als elementen uit het cartesisch product van twee of meerdere verzamelingen. Bijvoorbeeld:

\[A \times B = \{ (a,b)~|~a \in A, ~b \in B \}\]

\[A \times B \times C = \{ (a,b,c)~|~a \in A, ~b \in B, ~c \in C \}\]

Dit zijn de definities voor 2-tupels (t.t.z. koppels) en 3-tupels (t.t.z. drietallen). In het eerste voorbeeld is de eerste component van ieder koppel een element uit \(A\) en is de tweede component van ieder koppel een element uit \(B\). Bekende concrete voorbeelden van \(A \times B\) en \(A \times B \times C\) zijn \(\mathbb{R}^2\) en \(\mathbb{R}^3\) respectievelijk. Zo is bijvoorbeeld \(\mathbb{R}^3\) de verzameling van alle 3-tupels waarvan de componenten allen uit \(\mathbb{R}\) komen.

Tupels maken in Python {#tuppython}¶

Beschouw nu volgende Python code:

helium  = ("He", 2)
neon    = ("Ne", 10)
argon   = ("Ar", 18)
krypton = ("Kr", 36)
xenon   = ("Xe", 54)
radon   = ("Rn", 86)

noble_gasses = (helium, neon, argon, krypton, xenon, radon)

Hier worden \(7\) variabelen gedefinieerd die elk geassocieerd zijn met een tupel. De eerste \(6\) variabelen bevatten elke een 2-tupel uit str \(\times\) int. De laatste variabele bevat dan weer een 6-tupel waarvan de componenten 2-tupels zijn.

De algemene manier om waarden in een tupel te groeperen bestaat er dus in van de waarden te omringen met haakjes en ze te scheiden door komma’s. Er wordt gezegd dat we hiermee een nieuw tupel “maken”. Wat we doen door zo’n tupel te maken is eigenlijk de waarden samenlijmen tot één samengestelde waarde in ons Python geheugen. In de computerwetenschappen noemen we zo’n samengestelde waarden ook wel een datastructuur. Het tupel ("He",2) is eigenlijk een structuur die uit 2 componenten bestaat: een string "He" en een geheel getal 2. Vermits alle waarden in Python een type hebben, hebben ook tupelwaarden een type. Gebruik eens de functie type om het type van helium en noble_gasses op te vragen in de REPL!

type(helium)

tuple

type(noble_gasses)

tuple

Operaties op Tupels¶

Zoals we weten definieert ieder type een aantal operaties en functies die we op zijn waarden kunnen toepassen. Wat zijn dan de operaties en functies die op tupels van toepassing zijn? De drie belangrijkste worden hieronder besproken. We gebruiken de variabele noble_gasses zoals die hierboven gedefinieerd werd:

noble_gasses

(('He', 2), ('Ne', 10), ('Ar', 18), ('Kr', 36), ('Xe', 54), ('Rn', 86))

De indexering van tupels is een operatie die een component uit een tupel uitleest. Dat gebeurt met een expressie met vierkante haken zoals getoond in onderstaande experimentjes. noble_gasses[1] geeft bijvoorbeeld de eerste component terug van het tupel. Merk op dat we beginnen te tellen vanaf \(0\) (tot de lengte van het tupel min \(1\)).

Herinner dat noble_gasses een tupel van tupels is. noble_gasses[1] geeft de eerste component van het tupel terug. Dat is dus in dit geval opnieuw een tupel, namelijk het tupel (’Ne’, 10).

noble_gasses[1]

('Ne', 10)

noble_gasses[2]

('Ar', 18)

Indien het indexeren van een tupel een tupel oplevert, dan kunnen we dat op zijn beurt indexeren. We spreken in dit geval van een dubbele indexering. Dat wordt hieronder geïllustreerd. Dit principe is willekeurig diep toepasbaar. Indien t een tupel is dat tupels met tupels met tupels bevat, dan kunnen we bijvoorbeeld t[0][0][0][0] schrijven!

noble_gasses[1][0]

'Ne'

noble_gasses[5][1]

len is een functie die we op een tupel kunnen toepassen en die het aantal componenten van dat tupel weergeeft. Dat noemen we de lengte van het tupel. Bijvoorbeeld:

len(noble_gasses)

len(noble_gasses[0])

+ tenslotte is een operator die twee tupels aan elkaar lijmt. Merk op dat dit reeds de 5de betekenis is van de + operator die we kennen.

radon + neon

('Rn', 86, 'Ne', 10)

Functies en operatoren kunnen natuurlijk steeds aanleiding geven tot verkeerd gebruik. Uiteraard dienen we len toe te passen op waarden van het juiste type. Momenteel zijn dat tupels en strings (probeer het eens!). Later zullen we lijsten zien en zullen we len ook gebruiken om de lengte van een lijst te noteren. Het toepassen van len op, zeg maar, een geheel getal zal zoals verwacht een foutmelding opleveren. Iets leerrijker zijn de foutmeldingen die we kunnen krijgen bij het indexeren van tupels. Dat wordt hieronder geïllustreerd:

noble_gasses[6]

---------------------------------------------------------------------------
IndexError                                Traceback (most recent call last)
<ipython-input-107-0d34a7b24cda> in <module>
----> 1 noble_gasses[6]

IndexError: tuple index out of range

Herinner dat de geldige indices lopen van \(0\) tot de lengte van het tupel min 1. Dat wil zeggen dat we ons noble_gasses tupel mogen indexeren van \(0\) tot \(5\). Het gebruik van \(6\) als index levert dan ook een runtime fout op: Python klaagt dat de gebruikte index buiten het geldige bereik (Eng: range) valt.

Twee Randgevallen¶

Ten slotte vermelden we nog twee speciale tupels. Een eerste speciaal geval is het tupel (). Dit is het lege tupel (naar analogie met de lege verzameling in de wiskunde). Het is een tupel zonder componenten waarvoor iedere indexeringspoging tot een runtime fout zal leiden. Een tweede speciaal geval betreft het maken van een tupel dat slechts uit één component bestaat. Dit kunnen we niet gewoon maken met de uitdrukking (1). De afwezigheid van komma’s doet Python immers denken dat we hier gewoon het getal \(1\) tussen haakjes hebben gezet. Indien we uitdrukkelijk een tupel willen met één component erin dienen we een komma te gebruiken: (1,). Uiteraard is dit een tupel dat enkel en alleen met index \(0\) te indexeren valt.

()

()

(1)

(1,)

(1,)

Toepassing: De Tabel van Mendeljev¶

Tupels hebben het grote voordeel dat ze gebruikt kunnen worden om een hoop data (bijvoorbeeld een reeks getallen) kunnen samenlijmen in één enkele waarde. Deze waarde kunnen we dan met een variabelennaam zoals noble_gasses associëren. Het belangrijkste voordeel hiervan bestaat erin dat we gewoon deze naam dienen te vermelden en we meteen alle edelgassen in één ruk vasthebben. Anders zouden we in al onze Python code over edelgassen telkens \(6\) variabelennamen moeten vermelden. Een zeer illustratief voorbeeld hiervan krijgen we als we de gehele tabel van Mendeljev in één tupel voorstellen. Hieronder laten we (een deel van) een module zien met filenaam mendeljev.py. In deze module staat slechts één variabele gedefinieerd met naam elements. Deze variabele bevat één tupel met \(92\) componenten die de \(92\) eerste elementen uit het periodieke systeem voorstellen. Iedere component van dat tupel is opnieuw een tupel (bestaande uit \(5\) componenten) die de afkorting van het element, de naam van het element, het atoomnummer, de atoommassa en de groep van het element bevat.

elements = (('H',  'Hydrogen',      1,   1.0079,   1,  53),
            ('He', 'Helium',        2,   4.0026,  18,  27),
            ('Li', 'Lithium',       3,   6.9410,   1, 145),
            ('Be', 'Beryllium',     4,   9.0122,   2, 105),
            ('B',  'Boron',         5,  10.8110,  13,  85),
            ('C',  'Carbon',        6,  12.0107,  14,  70),
            ('N',  'Nitrogen',      7,  14.0067,  15,  65),
            ('O',  'Oxygen',        8,  15.9994,  16,  60),
            ('F',  'Fluorine',      9,  18.9984,  17,  50),
            ('Ne', 'Neon',         10,  20.1797,  18,  32),
            ('Na', 'Sodium',       11,  22.9897,   1, 180),
            ('Mg', 'Magnesium',    12,  24.3050,   2, 150),
            ('Al', 'Aluminum',     13,  26.9815,  13, 125),
            ('Si', 'Silicon',      14,  28.0855,  14, 110),
            ('P',  'Phosphorus',   15,  30.9738,  15, 100),
            ('S',  'Sulfur',       16,  32.0650,  16, 100),
            ('Cl', 'Chlorine',     17,  35.4530,  17, 100),
            ('Ar', 'Argon',        18,  39.9480,  18,  71),
            ('K',  'Potassium',    19,  39.0983,   1, 220),
            ('Ca', 'Calcium',      20,  40.0780,   2, 180),
            ('Sc', 'Scandium',     21,  44.9559,   3, 160),
            ('Ti', 'Titanium',     22,  47.8670,   4, 140),
            ('V',  'Vanadium',     23,  50.9415,   5, 135),
            ('Cr', 'Chromium',     24,  51.9961,   6, 140),
            ('Mn', 'Manganese',    25,  54.9380,   7, 140),
            ('Fe', 'Iron',         26,  55.8450,   8, 140),
            ('Co', 'Cobalt',       27,  58.9332,   9, 135),
            ('Ni', 'Nickel',       28,  58.6934,  10, 135),
            ('Cu', 'Copper',       29,  63.5460,  11, 135),
            ('Zn', 'Zinc',         30,  65.3900,  12, 135),
            ('Ga', 'Gallium',      31,  69.7230,  13, 130),
            ('Ge', 'Germanium',    32,  72.6400,  14, 125),
            ('As', 'Arsenic',      33,  74.9216,  15, 115),
            ('Se', 'Selenium',     34,  78.9600,  16, 115),
            ('Br', 'Bromine',      35,  79.9040,  17, 115),
            ('Kr', 'Krypton',      36,  83.8000,  18,  85),
            ('Rb', 'Rubidium',     37,  85.4678,   1, 235),
            ('Sr', 'Strontium',    38,  87.6200,   2, 200),
            ('Y',  'Yttrium',      39,  88.9059,   3, 180),
            ('Zr', 'Zirconium',    40,  91.2240,   4, 155),
            ('Nb', 'Niobium',      41,  92.9064,   5, 145),
            ('Mo', 'Molybdenum',   42,  95.9400,   6, 145),
            ('Tc', 'Technetium',   43,  98.0000,   7, 135),
            ('Ru', 'Ruthenium',    44, 101.0700,   8, 130),
            ('Rh', 'Rhodium',      45, 102.9055,   9, 135),
            ('Pd', 'Palladium',    46, 106.4200,  10, 140),
            ('Ag', 'Silver',       47, 107.8682,  11, 160),
            ('Cd', 'Cadmium',      48, 112.4110,  12, 155),
            ('In', 'Indium',       49, 114.8180,  13, 155),
            ('Sn', 'Tin',          50, 118.7100,  14, 145),
            ('Sb', 'Antimony',     51, 121.7600,  15, 145),
            ('Te', 'Tellurium',    52, 127.6000,  16, 140),
            ('I',  'Iodine',       53, 126.9045,  17, 140),
            ('Xe', 'Xenon',        54, 131.2930,  18, 102),
            ('Cs', 'Cesium',       55, 132.9055,   1, 260),
            ('Ba', 'Barium',       56, 137.3270,   2, 215),
            ('La', 'Lanthanum',    57, 138.9055,   3, 195),
            ('Ce', 'Cerium',       58, 140.1160, 101, 185),
            ('Pr', 'Praseodymium', 59, 140.9077, 101, 185),
            ('Nd', 'Neodymium',    60, 144.2400, 101, 185),
            ('Pm', 'Promethium',   61, 145.0000, 101, 185),
            ('Sm', 'Samarium',     62, 150.3600, 101, 185),
            ('Eu', 'Europium',     63, 151.9640, 101, 185),
            ('Gd', 'Gadolinium',   64, 157.2500, 101, 180),
            ('Tb', 'Terbium',      65, 158.9253, 101, 175),
            ('Dy', 'Dysprosium',   66, 162.5000, 101, 175),
            ('Ho', 'Holmium',      67, 164.9303, 101, 175),
            ('Er', 'Erbium',       68, 167.2590, 101, 175),
            ('Tm', 'Thulium',      69, 168.9342, 101, 175),
            ('Yb', 'Ytterbium',    70, 173.0400, 101, 175),
            ('Lu', 'Lutetium',     71, 174.9670, 101, 175),
            ('Hf', 'Hafnium',      72, 178.4900,   4, 155),
            ('Ta', 'Tantalum',     73, 180.9479,   5, 145),
            ('W',  'Tungsten',     74, 183.8400,   6, 135),
            ('Re', 'Rhenium',      75, 186.2070,   7, 135),
            ('Os', 'Osmium',       76, 190.2300,   8, 130),
            ('Ir', 'Iridium',      77, 192.2170,   9, 135),
            ('Pt', 'Platinum',     78, 195.0780,  10, 135),
            ('Au', 'Gold',         79, 196.9665,  11, 135),
            ('Hg', 'Mercury',      80, 200.5900,  12, 150),
            ('Tl', 'Thallium',     81, 204.3833,  13, 190),
            ('Pb', 'Lead',         82, 207.2000,  14, 180),
            ('Bi', 'Bismuth',      83, 208.9804,  15, 160),
            ('Po', 'Polonium',     84, 209.0000,  16, 190),
            ('At', 'Astatine',     85, 210.0000,  17,  -1),
            ('Rn', 'Radon',        86, 222.0000,  18,  -1),
            ('Fr', 'Francium',     87, 223.0000,   1,  -1),
            ('Ra', 'Radium',       88, 226.0000,   2, 215),
            ('Ac', 'Actinium',     89, 227.0000,   3, 195),
            ('Th', 'Thorium',      90, 232.0381, 102, 180),
            ('Pa', 'Protactinium', 91, 231.0359, 102, 180),
            ('U',  'Uranium',      92, 238.0289, 102, 175))

Hieronder laten we zien hoe we dit tupel kunnen gebruiken in de REPL nadat we de inhoud van de file hebben geïmporteerd. We zullen dit tupel later in de cursus nog een aantal keren gebruiken.

from mendeljev import *

len(elements)

koolstof = elements[5]

koolstof

('C', 'Carbon', 6, 12.0107, 14, 70)

Gevalsstudie: Matplotlib¶

We eindigen dit hoofdstuk met een gevalstudie die alles combineert wat we tot nu toe gezien hebben en die bovendien ook het nut van Python laat zien voor wetenschappers en ingenieurs. We gebruiken de Matplotlib bibliotheek om wetenschappelijke grafieken te tekenen.

Om met de deur in huis te vallen laten we meteen de kracht zien van de functies uit Matplotlib. Onderstaande figuur laat een plaatje zien (dat we overgenomen hebben van de homepage van Matplotlib) van het soort zeer professionele grafieken die we met Matplotlib kunnen maken. Het gebruiken van de bibliotheek op dit professioneel niveau vereist echter meer kennis van Python dan we tot nu toe gezien hebben. We gaan echter een paar grafieken maken die we met onze beperkte Python kennis nu reeds kunnen tekenen. De grafieken stellen bij voorbeeld meetwaarden voor van één of andere experiment in een laboratorium.

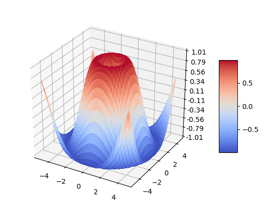
Grafieken Tekenen¶

De code hieronder laat alles zien wat we nodig hebben om een simpele grafiek te tekenen.

Eerst en vooral beginnen we met from matplotlib.pyplot import *. Dit zal alle functies en variabelen die opgeslagen zitten in de bibliotheek matplotlib.pyplot importeren in onze REPL. Deze bevat o.a. de functies plot en show die we nadien gebruiken.
Vervolgens importeren we alle functies en variabelen die opgeslagen zitten in de math bibliotheek. Dit is omdat we de sqrt functie zullen nodig hebben om vierkantswortels te berekenen.
Vervolgens zien we de functie plot twee keer aan het werk. Deze verwacht één argument; een tupel met de waarden die op de grafiek uitgezet dienen te worden. Merk op dat plot eigenlijk “tekent in het computergeheugen”. Het is show die effectief een figuur zal tonen op het scherm. Er zit machinerie achter deze notebooks die de figuur automatisch in de notebook toevoegt.

from matplotlib.pyplot import *
from math import *

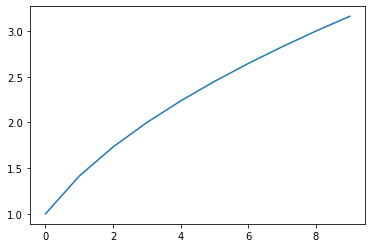
plot((1,2,3,4,5,6,7,8,9,10))
show()

plot((sqrt(1),sqrt(2),sqrt(3),sqrt(4),sqrt(5),sqrt(6),sqrt(7),sqrt(8),sqrt(9),sqrt(10)))
show()

Meerdere grafieken in 1 figuur¶

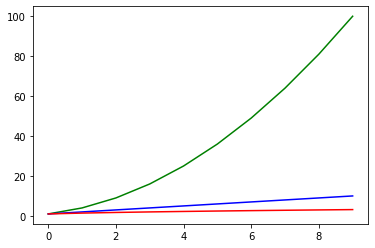
Omdat plot “tekent in het computergeheugen” en show “de figuur toont op het scherm” kan je drie keer plot aanroepen en dan pas show zodat je 1 figuur krijgt met 3 grafieken er in. plot neemt facultatief een aantal argumenten waaronder een argument om de kleur te kiezen. In onderstaand voorbeeld is gekozen voor “g” (groen-green), “b” (blauw-blue) en “r” (rood-red). De drie grafieken komen in 1 figuur terecht maar in verschillende kleuren.

plot((1,4,9,16,25,36,49,64,81,100),"g")
plot((1,2,3,4,5,6,7,8,9,10),"b")
plot((sqrt(1),sqrt(2),sqrt(3),sqrt(4),sqrt(5),sqrt(6),sqrt(7),sqrt(8),sqrt(9),sqrt(10)),"r")
show()

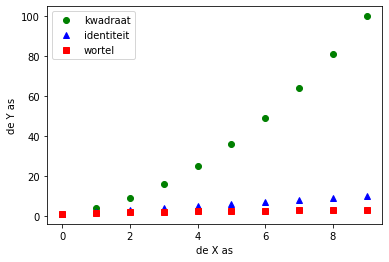
In het laatste voorbeel wordt samen met de kleur ook de manier van de grafiek te tekenen aangepast. “go”,”b^” en “rs” staan voor groene circeltjes, blauwe driehoekjes en rode vierkantjes. Er zijn ook labels aan de X- en Y-as toegevoegd en er is een legend naast de grafiek gezet. We verwijzen naar de online documentatie van Matplotlib voor een volledige beschrijving van alle mogelijke geldige formateringsstrings.

plot((1,4,9,16,25,36,49,64,81,100),"go", label='kwadraat')
plot((1,2,3,4,5,6,7,8,9,10),"b^", label='identiteit')
plot((sqrt(1),sqrt(2),sqrt(3),sqrt(4),sqrt(5),sqrt(6),sqrt(7),sqrt(8),sqrt(9),sqrt(10)),"rs", label='wortel')
xlabel('de X as')
ylabel('de Y as')
legend()
show()

Functies vs. Procedures¶

Het vorige voorbeeld toont aan dat Python functies niet alleen gebruikt kunnen worden om een waarde te berekenen (zoals bijvoorbeeld sqrt dat doet) maar ook om Python gewoon te bevelen om iets te doen. Zo geeft de aanroep van plot geen waarde terug. De functie zal echter wel iets nuttig doen (in dit geval tekenen) maar vervolgens geen resultaatwaarde teruggeven. Hetzelfde geldt voor show. In de computerwetenschappen worden functies zonder resultaat vaak procedures genoemd omdat ze eigenlijk — door ze aan te roepen — een proces uitvoeren. Alhoewel alle Python functies technisch hetzelfde zijn zullen we functies zonder resultaat dus voortaan procedures noemen. (Later zullen we zien dat eigenlijk toch de waarde None wordt teruggegeven maar dat de REPL deze waarde nooit print.)

Ten slotte nog een laatste inzicht. We hebben eerder het verschil gemaakt tussen expressies en statements. Expressies hebben een waarde maar statements niet. Met onze nieuwe terminologie kunnen we dus zeggen dat een functie-aanroep een expressie is. De functie-aanroep heeft een waarde, namelijk de waarde die door de functie wordt teruggegeven. Een procedure-aanroep is een statement aangezien hier geen waarde uitkomt. In ons voorbeeld zijn de aanroepen van sqrt dus expressies. De aanroepen van plot en sqrt zijn statements aangezien geen van beide een resultaatwaarde weergeven.

Samenvatting¶

In dit topic hebben de eerste stappen gezet in Python. We hebben gezien dat Python bestaat uit expressies en statements. Expressies hebben een waarde en statements bevelen de Python REPL om iets te doen maar hebben geen waarde. De verschillende soorten Python waarden die we tot nu toe gezien hebben zijn gehele getallen, floating point getallen, complexe getallen, strings en tupels. Tupels zijn samengestelde waarden waarvan de samenstellende componenten opnieuw waarden zijn (en dus opnieuw tupels kunnen zijn). Technisch noemen we al deze soorten “types”.

Operatoren en functies zijn de werkpaarden van Python. We kunnen ze toepassen op één of meerdere waarden. Functies die geen resultaat opleveren maar “gewoon iets doen” noemen we procedures.

Variabelen zijn zelfgekozen namen en worden op ieder moment geassocieerd met een waarde. Het assignment statement wordt zowel gebruikt om nieuwe variabelen te definiëren als om de waarde van een reeds gedefinieerde variabele te veranderen.

Ten slotte hebben we gezien hoe we modules die door anderen (of door onszelf) zijn geschreven kunnen importeren. Dat kan gebeuren met verschillende varianten van het import statement. Modularisatie is een heel krachtige techniek in programmeren en laat toe om de complexiteit van heel grote programma’s te gaan beheersen.

Inleiding tot de Computerwetenschappen

TOPIC 2: Basis Python¶

De Read-Eval-Print Lus¶

Read¶

Eval¶

Print¶

Whitespace¶

Python Expressies, Waarden en Types¶

Types¶

Reele vs. float getallen¶

Complexe Getallen¶

Strings¶

Samenvatting¶

Functies en Operators¶

Ingebouwde Functies Oproepen¶

Voorrangsregels op Operatoren¶

Ingebouwde Functies en Operatoren¶

Variabelen¶

De Toekenning¶

Statements¶

Toekenning (vervolg)¶

Constanten¶

Modules¶

Een module importeren¶

Een andere naam kiezen voor een module¶

De inhoud van een module importeren¶

Zelf een module maken (en importeren)¶

Samenvatting¶

Tupels¶

Tupels maken in Python {#tuppython}¶

Operaties op Tupels¶

Twee Randgevallen¶

Toepassing: De Tabel van Mendeljev¶

Gevalsstudie: Matplotlib¶

Grafieken Tekenen¶

Meerdere grafieken in 1 figuur¶

Functies vs. Procedures¶

Samenvatting¶

Reele vs. `float` getallen¶