TOPIC 4: Recursieve Functies¶

In dit topic behandelen we zogenoemde recursieve functies. In het vorige topic bespraken we functies die voor gegeven invoerwaarden (d.w.z. de argumenten) na een korte berekening meteen de uitvoerwaarde teruggeven. Zo geeft bijvoorbeeld to_celcius meteen de temperatuur in Celcius terug bij toepassing van de functie op een gegeven temperatuur in Fahrenheit. De tijd die Python nodig heeft om deze waarde te berekenen is verwaarloosbaar: moderne computers zijn immers in staat om optellingen, aftrekkingen, vermenigvuldigingen en delingen zéér snel uit te voeren. In de REPL is het alsof Python de resultaatwaarde meteen klaar heeft. Voor recursieve functies is dit niet langer het geval. Zoals we zullen zien zullen recursieve functies een tijdje “bezig” zijn alvorens ze een resultaat opleveren. De computer is dan bezig met een (langdurig) computationeel proces.

Zoals we zullen zien bestaan er verschillende soorten computionele processen die door recursieve functies opgewekt worden. De classificatie van deze soorten processen wordt bepaald door de tijd die nodig is om het proces uit te voeren. Immers, “time is money” en dat geldt ook voor de tijd die we computers laten rekenen. In dit topic ontwikkelen we drie technieken die ons zullen toelaten om een beter inzicht te krijgen in de duur van een computationeel proces. Met tracing zorgen we ervoor dat een lopend proces tijdens de uitvoering een spoor achterlaat op het scherm. Met profiling gaan we de tijd effectief meten voor verschillende invoerwaarden en deze in een klassieke grafiek uitzetten. Met de Big Oh notatie gaan we de tijdsduur van een proces neerschrijven in de vorm van een wiskundige uitdrukking.

Recursie en Recursieve Processen¶

Je hebt waarschijnlijk al over $n!$, de faculteit van een getal $n$, gehoord. Bijvoorbeeld: $5! = 5 \times 4 \times 3 \times 2 \times 1$. In het algemeen stelt men dikwijls dat $n! = n \times (n-1) \times ... \times 2 \times 1$. Zo’n definitie met “drie puntjes” erin wordt echter niet als voldoende precies beschouwd door wiskundigen en nog veel minder door computerwetenschappers. Een veel betere definitie van de faculteit is volgende zogenaamde inductieve definitie:

\[\begin{split}n! = \left\{ \begin{array}{ll} 1 & als~n=0 \\ n.(n-1)! & als~n > 0 \end{array}\right.\end{split}\]

Deze vergelijking definieert de faculteit op een precieze manier. De definitie gebeurt echter in termen van zichzelf: de faculteit komt zowel aan de linkerkant als aan de rechterkant van het $=$ teken voor. Gelukkig zit de definitie goed in mekaar omdat (a) er een eindvoorwaarde is om de circulariteit te stoppen (namelijk “$n=0$”) en (b) het getal aan de rechterkant steeds kleiner is dan het getal aan de linkerkant en daardoor de eindvoorwaarde vroeg of laat wordt bereikt.

In Python kan men zo’n inductieve definitie quasi rechttoe rechtaan vertalen als volgt:

def fac(n):
    

def fac(n):
    if n==0:
        return 1
    else:
        return n*fac(n-1)

fac(5)

We schrijven dus een functie fac die 2 gevallen onderscheidt. In het algemene geval roept fac zichzelf op maar er is echter een eindvoorwaarde (ook stopconditie genoemd) om deze circulariteit te stoppen. Het toepassen van fac op bijvoorbeeld 5 zal fac toepassen op 4 wat fac zal toepassen op 3 enzovoort. Uiteindelijk wordt fac toegepast op 0 wat 1 teruggeeft. Dan begint het omgekeerde proces: iedere toepassing van fac op n-1 krijgt een resultaat terug, vermenigvuldigt het met n en geeft dit als resultaat terug naar het niveau ervoor.

In de computerwetenschappen noemt men zo’n inductieve definitie traditioneel een recursieve definitie. Dit is verwant met het Engelse “to re-occur” aangezien de naam fac in de functie body opnieuw voorkomt.

Procesvisualisatie: Tracing¶

In het vorige topic was het vrij eenvoudig om het gedrag van een functie te begrijpen: je stopt er argumenten in, de functie rekent iets uit en je krijgt de resultaten meteen terug. fac is een allereerste voorbeeld van een functie die aanleiding geeft tot wat we een computationeel proces noemen: onze Python REPL is een tijdje bezig met allerlei ingewikkelde dingen en pas na afronding ervan krijgen we een resultaat. Zoals we nu zullen zien is het bijzonder nuttig om een goed inzicht te hebben in de precieze aard van dit computationele proces en dan vooral in de tijdsduur die het proces in beslag zal nemen.

Om te begrijpen wat er precies gebeurt zullen we vooreerst het proces proberen te visualiseren. We bestuderen 2 procesvisualizatietechnieken: tracing en profiling. We beginnen met tracing. Een trace van een programma krijgen we wanneer het programma een spoor van zijn activiteiten achterlaat op het scherm. Bedoeling is dus dat het programma nu en dan iets op het scherm zet om ons te vertellen wat het aan het doen is.

Laten we er op dit moment gewoon even van uitgaan dat we erin geslaagd zijn een andere versie traced_fac te schrijven die als volgt werkt.

Elke keer we traced_fac oproepen print die meteen een boodschap op het scherm calling fac with n= w waarbij w de waarde heeft die de functie zonet als actuele parameter ontving.
Net voor het terugkeren print traced_fac nog een andere boodschap returning from fac with r waarbij r de terugkeerwaarde op dat moment is.

We zorgen er bovendien voor dat we telkens een beetje meer inspringen bij iedere nieuwe oproep van traced_fac zodat het inspring-niveau van een oproep precies één streepje meer print dan het inspring-niveau van de oproeper van die oproep. We gaan later die traced_fac eens uitpluizen maar om de aandacht niet af te leiden van het onderwerp dat we nu aan het behandelen zijn importeren we die gewoon uit een een klaargezette module.

Hieronder laten we wel zien wat er op je scherm verschijnt als je traced_fac(5) oproept. Het uiteindelijke resultaat van de functieoproep 120 wordt zoals steeds door de REPL geprint.

from tracing import *

traced_fac(7)

calling fac with n= 7
-calling fac with n= 6
--calling fac with n= 5
---calling fac with n= 4
----calling fac with n= 3
-----calling fac with n= 2
------calling fac with n= 1
-------calling fac with n= 0
-------returning from fac with 1
------returning from fac with 1
-----returning from fac with 2
----returning from fac with 6
---returning from fac with 24
--returning from fac with 120
-returning from fac with 720
returning from fac with 5040

Wat leren we uit zo’n trace? We zien duidelijk dat het aantal recursieve toepassingen van traced_fac (en dus ook fac) precies gelijk is aan $n+ 1$. Voor iedere recursieve functie waarbij het aantal functieoproepen van de vorm $a.n+b$ is zeggen we dat ze aanleiding geeft tot een lineair recursief proces. In ons geval is $a=b=1$ maar dat kunnen andere constanten zijn. Het basisinzicht is dat de afhankelijkheid lineair is. Dat wil zeggen dat het proces ongeveer $k$ keer zolang gaat duren indien we de input $k$ keer zo groot maken. Dubbel zo grote invoer geeft dus dubbel zoveel werk, drie keer zo grote invoer geeft drie keer zoveel werk, enz. Op het eerste zicht is dat misschien triviaal, maar zoals we zo meteen zullen zien is dat lang niet altijd het geval.

Procesvisualisatie: Profiling¶

Een tweede manier om deze informatie te laten zien bestaat erin om gewoon de echte tijd te meten die de fac functie heeft gespendeerd tijdens een bepaalde oproep. Dit geeft ons voor iedere n die we uitproberen een uitvoeringstijd (bvb. in milliseconden). Zulks meten van de rekentijd van een functie voor verschillende soorten invoer noemen we profilen van de functie. Op het eerste zicht dienen we dan met een chronometer elke uitvoering afzonderlijk te timen. Dit zou echter een zeer omslachtige en onhandige manier van werken zijn. We kunnen hiervoor beter Python zelf gebruiken. Computers zijn immers perfect in staat om de tijd te meten van het computationeel process dat ze zelf aan het uitvoeren zijn. We zullen hiervoor de module time gebruiken maar opnieuw, om de aandacht niet af te leiden van het onderwerp dat we nu aan het behandelen zijn stoppen we dat detail nu even weg in een module profiling.

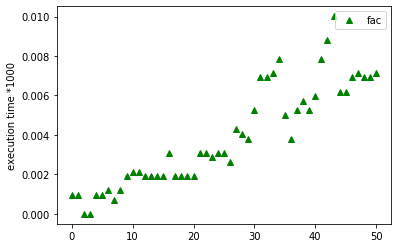
Onderstaande figuur laat een grafiek zien waarbij we de fac functie toegepast hebben op verschillende invoerwaarden variërend van $0$ tot $50$. Ook in de profile zien we dat fac een lineair proces genereert. De grafiek laat min of meer een rechte zien.

from profiling import *

plot_fac(50)

'fac'

De computer is bijzonder snel. Op de getoonde grafiek zijn de tijdsmetingen al vermenigvuldigd met een factor 1000. Ook is niet een éénmalige meting van elke fac(n) oproep gebruikt maar is een gemiddelde van 100 keer meten genomen. Zelfs dan zitten er in de grafiek een aantal aberraties. Die zijn een gevolg van het feit dat een computer tegenwoordig met veel verschillende taken tegelijk bezig is. De processor (of in moderne PC’s zelfs de meerdere processors) moet zijn tijd dan ook zo eerlijk mogelijk verdelen tussen de verschillende taken waaraan gewerkt wordt. Hierdoor kan het zijn dat we bijvoorbeeld een meting doen voor fac net op het ogenblik dat de computer iets anders aan het doen was (bv. mail binnenhalen van een server). Die specifieke uitvoering van fac kan dan beduidend trager zijn dan “normaal”. Dit verklaart de uitschieters en onregelmatigheden in de grafiek. Je kan als experiment bovenstaande plot een paar keer achter elkaar oproepen (door de cel een paar keer te “runnen”). Ja zal zien dat de grafiek telkens wat verschilt.

Soorten Computationele Processen¶

Niet iedere recursieve functie geeft automatisch aanleiding tot een lineair recursief proces. Zoals we in deze sectie zullen zien zijn sommige processen slim in de zin dat ze minder en minder extra recursieve aanroepen genereren naarmate de invoer groter en groter wordt. We zullen als voorbeeld logaritmische processen bestuderen. Andere functies zijn dan weer bijzonder dom en genereren steeds meer extra recursieve aanroepen bij grotere invoer. Als voorbeeld van zulke processen zullen we exponentiële processen bestuderen.

Logaritmische Processen¶

Laten we nog een tweede voorbeeld bestuderen van een functie die aanleiding geeft tot een lineair proces. Alhoewel Python reeds de ingebouwde ** operator kent voor de machtsverheffing (t.t.z. 2**5 betekent $2^5$) zullen we ons nu op het zélf programmeren van deze operatie toespitsen.

Een eenvoudige inductieve definitie van $a^n$ voor een reëel getal $a$ en een natuurlijk getal $n$ zou er als volgt kunnen uitzien:

\[\begin{split}a^n = \left\{ \begin{array}{ll} 1 & als & n=0 \\ a . a^{(n-1)} & anders \end{array}\right.\end{split}\]

In gewoon Nederlands drukt deze definitie niks anders uit dan het feit dat we een machtsverheffing kunnen definiëren als een reeks van opeenvolgende vermenigvuldigingen. Deze inductieve definitie vertaalt zich net zoals fac rechttoe rechtaan in een recursieve Python functie:

def power(a,n):
    if n == 0: 
        return 1
    else: 
        return a * power(a, n-1)

power(2,7)

Net zoals onze fac zal de functie power aanleiding geven tot een lineair recursief proces. Hoe groter de invoer, hoe groter het aantal recursieve toepassingen, en bovendien is het verband lineair: bij een $n$ die $k$ keer zo groot is zullen we ongeveer $k$ keer zoveel oproepen genereren. Dat wordt geïllustreerd door een getracete versie van power(detail later). Opnieuw laten we traced_power iets afdrukken op het scherm net voor het rekenwerk en net voor het uitvoeren van het return statement. Het uiteindelijke resultaat van de functieoproep 128 wordt zoals steeds door de REPL geprint.

traced_power(2,7)

calling power with n= 7
-calling power with n= 6
--calling power with n= 5
---calling power with n= 4
----calling power with n= 3
-----calling power with n= 2
------calling power with n= 1
-------calling power with n= 0
-------returning from power with 1
------returning from power with 2
-----returning from power with 4
----returning from power with 8
---returning from power with 16
--returning from power with 32
-returning from power with 64
returning from power with 128

Kunnen we beter? Het antwoord op deze vraag is een volmondig “ja”! Om de oplossing te zien is het belangrijk te weten dat $a^n = (a^{\frac{n}{2}})^2$ voor elke even $n$. Bijvoorbeeld $a^6 = (a^3)^2$. Dit is natuurlijk enkel mogelijk als $n$ een even getal is. In het geval dat $n$ oneven is, kiezen we voor de originele aanpak. Dit brengt ons bij de volgende inductieve definitie. Ze is opgevat als een gevalsanalyse met 3 verschillende takken. De twee laatste zijn de eigenlijke inductieve stappen. De eerste is de eindstap van de inductie.

\[\begin{split}a^n = \left\{ \begin{array}{ll} 1 & als~n=0 \\ (a^{\frac{n}{2}})^2 & als~n~even~is \\ a.a^{n-1} & anders \end{array}\right.\end{split}\]

Ook deze inductieve definitie is quasi rechttoe rechtaan om te zetten naar Python. Vermits we deze keer 3 opties hebben, leidt dit naar een if-constructie met 3 takken. Dit resulteert in de volgende fast_power functie waarvan we de naam zo meteen zullen verklaren.

def fast_power(a,n):
    if n == 0: 
        return 1
    elif n%2 == 0: 
        return fast_power(a,n/2) ** 2
    else: 
        return a * fast_power(a,n-1)

fast_power(2,7)

Gegeven een $n$, hoe dikwijls wordt fast_power opgeroepen? We kunnen opnieuw overgaan tot tracing en profiling van de functie om haar gedrag te bestuderen. Een getracete versie van fast_power geeft volgend resultaat op het scherm:

traced_fast_power(2,7)

calling fast_power with n= 7
-calling fast_power with n= 6
--calling fast_power with n= 3.0
---calling fast_power with n= 2.0
----calling fast_power with n= 1.0
-----calling fast_power with n= 0.0
-----returning from fast_power with 1
----returning from fast_power with 2
---returning from fast_power with 4
--returning from fast_power with 8
-returning from fast_power with 64
returning from fast_power with 128

Op het eerste zicht zien we nauwelijks verbetering: voor $n=7$ tellen we een totaal aan $6$ oproepen. Enkel de oproepen met $n=5$ en $n=4$ worden uitgespaard. Maar laten we nu eens traced_fast_power oproepen met een wat grotere $n$, bijvoorbeeld $n=25$. De trace ziet er als volgt uit:

traced_fast_power(2,25)

calling fast_power with n= 25
-calling fast_power with n= 24
--calling fast_power with n= 12.0
---calling fast_power with n= 6.0
----calling fast_power with n= 3.0
-----calling fast_power with n= 2.0
------calling fast_power with n= 1.0
-------calling fast_power with n= 0.0
-------returning from fast_power with 1
------returning from fast_power with 2
-----returning from fast_power with 4
----returning from fast_power with 8
---returning from fast_power with 64
--returning from fast_power with 4096
-returning from fast_power with 16777216
returning from fast_power with 33554432

33554432

Voor de gewone power verwachten we 26 oproepen. Nu zien we echter slechts 9 oproepen! De functie maakt enorme sprongen voorwaarts bij ieder even getal. Grote delen van het originele rekenwerk worden dus overgeslagen. Dit wordt nóg duidelijker als we een profile opstellen van power en het contrasteren met een profile van fast_power. Onderstaande figuur laat de grafiek zien van de resultaten bij het opmeten van de uitvoeringstijd van power en fast_power voor een vast grondtal $a$ en een exponent $n$ die varieert van $0$ tot $50$. Ook hier zie je wat uitschieters en onregelmatigheden in de grafiek. Je kan als experiment bovenstaande plot een paar keer achter elkaar oproepen (door de cel een paar keer te “runnen”). Ja zal zien dat de grafiek telkens wat verschilt.

plot_power(2, 50)

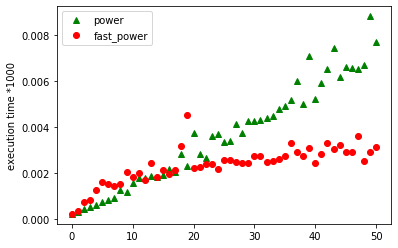
De resultaten laten opnieuw zien hoe lang (uitgedrukt in milliseconden maal 1000) het duurt om bij een gegeven $n$ beide functies uit te voeren. De bovenste grafiek is een gewone lineaire grafiek die we al zagen bij fac. Het is quasi dezelfde lineaire grafiek die wordt opgeleverd voor power aangezien de code eigenlijk dezelfde opbouw heeft: we hebben een recursie die in iedere oproep de variabele $n$ met één vermindert en stopt indien $n=0$. De grafiek die eronder ligt is het resultaat voor fast_power. Deze grafiek lijkt verdacht veel op de grafiek voor $log(x)$! Hoe verklaren we dit zogenoemde logaritmisch gedrag van fast_power?

Beschouw het geval dat $n$ een perfecte macht van $2$ is, t.t.z. $n=2^k$ voor zekere $k$. Bij een eerste oproep van fast_power zal (vermits $n$ even is), de exponent door twee gedeeld worden zodat de volgende aanroep met $2^{k-1}$ gebeurt. Aangezien dit getal steeds even blijft, blijven we delen door $2$. Het is duidelijk dat dit in totaal $k$ keer zal gebeuren. Vermits $n=2^k$, krijgen we dus $k=log_2(n)$ wegens de definitie van $log$. Indien $n$ geen perfecte macht van $2$, dan gaat de redenering als volgt. Tijdens het proces delen we door $2$ indien $n$ even is en trekken we $1$ af als $n$ oneven is. Maar indien $n$ oneven is, zal ze de volgende keer wel gegarandeerd even zijn. Dus gaan we maximaal $log_2(n)$ keer $1$ aftrekken. In totaal wordt het maximaal aantal oproepen dus begrensd door $log_2(n)$ keer delen door $2$ en eventueel (daartussen) $log_2(n)$ keer aftrekken. De totale hoeveelheid oproepen is dus maximaal $2.log_2(n)$ wat nog steeds logaritmisch is.

Dit is bijzonder goed nieuws aangezien de $log_2(n)$ grafiek veel trager stijgt dan de grafiek voor $n$. In een logaritmisch proces word je dus nauwelijks afgestraft voor het oproepen van de functie met grote waarden. Logaritmische processen zijn dan ook bijzonder fel gegeerd door computerwetenschappers.

Exponentiële Processen¶

De vorige sectie liet zien dat er recursieve functies bestaan die logaritmische processen (t.t.z. sublineaire; minder dan lineair) opleveren. Er bestaan ook recursieve functies die veel trager zijn dan het lineaire geval. Beschouw volgende definitie van de zogenoemde Fibonacci getallen:

\[\begin{split}f_n = \left\{ \begin{array}{ll} 0 & als & n=0 \\ 1 & als & n=1 \\ f_{n-1} + f_{n-2} & anders \end{array}\right.\end{split}\]

Deze rij getallen (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ….) wordt ook wel de konijnenrij genoemd. Indien we beginnen zonder konijnen en in de eerste maand één paar konijnen hebben, krijgen we de rij als het aantal paren konijnen in elke maand. De simplistische aanname is dat er geen konijnen sterven. Het idee is dat een konijn een maand nodig heeft om volwassen te worden en dat elk paar konijnen iedere maand een paar nakomelingen krijgt. Het aantal paren in maand $n$ is dus precies het aantal paren van de vorige generatie plus het aantal paren dat ouder is dan 2 maanden.

Het is opnieuw een eenvoudig klusje om deze inductieve definitie naar Python om te zetten. Hier is het resultaat:

def fib(n):
    if n==0:
        return 0
    elif n==1:
        return 1
    else:
        return fib(n-1)+fib(n-2)

fib(5)

In deze functie geeft elke oproep aanleiding tot twee recursieve oproepen en worden de resultaten van beide oproepen nadien met mekaar gecombineerd (m.b.v. +) waarna het gecombineerde resultaat wordt teruggegeven.

Wat kunnen we zeggen over het aantal recursieve oproepen gegeven een zekere $n$? We zullen de zaak opnieuw onderzoeken met behulp van tracing en profiling. We beginnen met een trace. Opnieuw gaan we ervan uit dat we een versie traced_fib hebben die een spoor op het scherm achterlaat net bij het binnenkomen en net voor het verlaten van een functie oproep. Hieronder zien we het resultaat voor $n=5$. Het resultaat van de functieaanroep 5 wordt zoals steeds door de door de REPL afgedrukt.

traced_fib(5)

calling fib with n= 5
-calling fib with n= 4
--calling fib with n= 3
---calling fib with n= 2
----calling fib with n= 1
----returning from fib with 1
----calling fib with n= 0
----returning from fib with 0
---returning from fib with 1
---calling fib with n= 1
---returning from fib with 1
--returning from fib with 2
--calling fib with n= 2
---calling fib with n= 1
---returning from fib with 1
---calling fib with n= 0
---returning from fib with 0
--returning from fib with 1
-returning from fib with 3
-calling fib with n= 3
--calling fib with n= 2
---calling fib with n= 1
---returning from fib with 1
---calling fib with n= 0
---returning from fib with 0
--returning from fib with 1
--calling fib with n= 1
--returning from fib with 1
-returning from fib with 2
returning from fib with 5

Indien we de trace op zijn kant zetten zien we duidelijk dat er een zogenoemde boom ontstaat doordat opeenvolgende oproepen steeds “dieper” gaan. Bovendien geven beide oproepen op hetzelfde niveau aanleiding tot twee takken die op datzelfde niveau in de boom vertrekken. Indien we die boom netjes tekenen krijgen we onderstaande figuur

Men zegt dan ook dat fib een boomrecursieve functie is. In het algemeen spreekt men van een boomrecursie van zodra een oproep van een functie resulteert in 2 of meer recursieve oproepen.

Maar welk soort computationeel proces zal fib nu genereren? De boom uit bovenstaande figuur hangt een beetje door aan de linkerkant. Hij is niet symmetrisch en het aantal vertakkingen in de boom berekenen is daarom niet zo eenvoudig. Om de analyse te vergemakkelijken bekijken we even de volgende “valse fib” vfib” waarbij we de oproep van fib(n-2) vervangen hebben door een tweede oproep van fib(n-1).

def vfib(n):
    if n==0:
        return 0
    elif n==1:
        return 1
    else:
        return vfib(n-1)+vfib(n-1)

We zouden natuurlijk evengoed return 2*vfib(n-1) kunnen schrijven en hetzelfde uitkomen, maar het is net de bedoeling van dit gedachtenexperiment om het boomrecursieve proces te vereenvoudigen maar wel degelijk te behouden. De omzetting naar return 2*vfib(n-1) zou weliswaar dezelfde uitkomst opleveren maar zou een lineair recursief proces opleveren en het is juist onze bedoeling om het boomrecursieve proces te bestuderen.

De hamvraagis: hoe dikwijls roept vfib zichzelf op? Het is duidelijk dat voor zeker $n$, er telkens exact $2$ oproepen met $n-1$ gegenereerd worden, en dus $4$ oproepen met $n-2$ enzoverder. In totaal zal vfib zichzelf $2^n-1$ keer oproepen vanaf $n \geq 2$. Men spreekt dan ook over een exponentieel proces.

plot_fib(10)

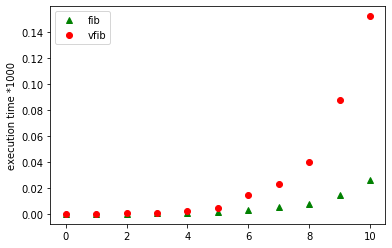
Bovenstaande figuur laat de resultaten zien van het profilen van zowel fib als vfib. Zoals we kunnen zien is de grafiek voor vfib (met de bolletjes) steiler dan de grafiek voor fib (met driehoekjes). Dit is eenvoudig te begrijpen als we zien hoe vfib tot stand is gekomen. We hebben immers fib(n-1)+fib(n-2) vervangen door vfib(n-1)+vfib(n-1). fib gaat dus één keer zeer diep en één keer ietsje minder diep in de recursie. vfib gaat twee keer zeer diep. De recursieboom van vfib is dan ook volledig symmetrisch. Maar beide grafieken tonen een duidelijke weergave van de exponentiële functie $f(x) = c^x$ voor één of andere constante $c$. Voor onze valse vfib is $c=2$. Met wat hardere wiskunde kan men aantonen dat fib zichzelf door de band $1,62^n$ keer aanroept maar de afleiding hiervan valt buiten het bestek van deze cursus. Zowel fib als vfib zijn dus exponentiële processen en dat is zeer slecht nieuws: zoals we aan de grafiek kunnen zien wordt de situatie voor relatief kleine $n$ al gauw onhandelbaar en duurt het zeer lang alvorens een resultaat wordt teruggegeven. Exponentiële processen worden door computerwetenschappers dan ook als leuk speelgoed aanzien dat in de praktijk absoluut moet worden vermeden. Hun uitvoering duurt zelfs voor redelijke keuzes van $n$ immers veel te lang.

Merk op dat dit geen intrinsiek kenmerk is van Fibonacci getallen maar wel van één bepaalde uitwerking ervan. Er bestaat ook uitwerkingen van fib die een lineair proces opleveren. We laten het aan de nieuwsgierige student over om zich ervan te vergewissen dat onderstaande code effectief de Fibonaccirij oplevert en bovendien een lineair proces genereert.

def fib_linear(a,b,n):
    if n==0:
        return a
    else:
        return fib_linear(b,a+b,n-1)
    
def fib(n):
    return fib_linear(0,1,n)

fib(5)

Traces en Profiles maken in Python¶

Laat ons nu eens kijken naar de manier waarop we een gegeven Python functie kunnen tracen en profilen.

Tracing¶

Onderstaande code laat een getracete versie van fac zien. De functie heet traced_fac en roept meteen een hulpfunctie fully_traced_fac op. Deze hulpfunctie heeft $2$ i.p.v. $1$ parameters. De eerste parameter is nog steeds de $n$ die nodig is om de faculteit te berekenen. De tweede parameter is een getal dat aangeeft hoeveel streepjes er geprint dienen te worden om in te springen bij het printen van de trace (Eng.: to indent = inspringen).

def traced_fac(n):
    return fully_traced_fac(n,0)

def fully_traced_fac(n,indent):
    print ("-"*indent + "calling fac with n=", n)
    if n == 0:
        res = 1
    else:
        res = n * fully_traced_fac(n-1,indent+1)
    print ("-"*indent + "returning from fac with", res)
    return res

Telkens we de functie fully_traced_fac aanroepen, zal zij meteen een boodschap op het scherm drukken: indent streepjes, gevolgd door calling fac with n=, gevolgd door de huidige waarde van n. Dan gebeurt de eigenlijke berekening van de faculteit op recursieve manier. We roepen de functie recursief op met n-1 en met indent+1 zodat het volgende inspringniveau één streepje meer zal genereren. Het resultaat van de berekening kennen we toe aan de variabele res. Dit is nodig aangezien we eerst nog een deel van de trace moeten printen alvorens we het resultaat kunnen teruggeven met return. Na het if statement wordt de trace dus afgemaakt en wordt het resultaat vervolgens teruggegeven uit de functie.

In iedere recursieve stap wordt er dus vóór en ná het berekenen een boodschap geprint die met het correcte aantal streepjes wordt ingesprongen. Tussen het printen van beide boodschappen worden de boodschappen van de recursieve oproepen geprint.

traced_power, traced_fast_power en traced_fib worden op equivalente manier geschreven. Alle 4 de functies zijn weggeschreven in een (zelfgemaakte) module tracing zodat ze in de secties hierboven konden geïmporteerd worden.

Profiling¶

Het maken van de profile is eigenlijk eenvoudiger dan het opstellen van de trace. De grafiek wordt gemaakt m.b.v. Matplotlib die we vroeger al gebruikt hebben. We gaan ook de module time gebruiken die is meegeleverd met Python.

import matplotlib.pyplot as plt
import time

Om voor een zekere $n$ te weten hoeveel tijd fac spendeert aan het uitrekenen van fac(n) kunnen we beroep doen op de een functie time (in de module time) die geen enkel argument vereist. Oproep van time.time() geeft het aantal milliseconden die verlopen zijn na 1 januari $1970$ ($0$ uur). We kunnen dus op zeer eenvoudige wijze bepalen hoelang fac nodig heeft om de faculteit uit te rekenen van een gegeven n: we bepalen de tijd t1, we rekenen fac uit (maar we gebruiken het resultaat niet aangezien het ons op dit moment niet interesseert), we bepalen opnieuw de tijd t2 en we geven het tijdsverschil tussen de twee tijden terug. Onderstaande functie timed_fac doet dat netjes. We vermenigvuldigen de gemeten tijd met een factor 1000 omdat de gemeten tijden echt heel klein zijn en we afrondfouten willen vermijden in latere berekeningen.

def timed_fac(n):
    t1 = time.time()
    fac(n)
    t2 = time.time()
    return (t2 - t1) * 1000

Om een grafiek te tekenen hebben we een tupel of een lijst van meetwaarden nodig als input voor de plot functie. Lijsten komen pas in een later topic aan bod. We behelpen ons hier met tupels. Onderstaande functie levert een tupel van 51 tijdsmetingen op, telkens voor een oproep van fac(n) met een invoerwaarde $n$ varierend van 0 tot 50.

def serie_timed_fac(high):
    result = ()
    for n in range(0,high+1):
        result = result + (timed_fac(n),) 
    return result

Tenslotte kunnen we de plot maken door de juiste procedures uit Matplotlib te gebruiken. Hier is de code om de plot voor fac op het scherm te krijgen.

def plot_fac(max):
    y_values = serie_timed_fac(max)
    plt.plot(y_values, 'g^', label='fac')
    plt.ylabel('execution time *1000')
    plt.legend()
    plt.show()        
    return "fac"

plot_fac(50)

'fac'

We kunnen we om de grilligheid van de timing die voorkomt uit het feit dat de computer tegelijk aan andere dingen aan het werken is enigzins proberen te dempen door een serie tijdsmetingen meerdere keren op te nemen en dan een gemiddelde te berekenen. Deze code kan heel compacte geschreven worden als we lijsten en list comprehensions kennen. We leggen de code om dit te doen uit als voorbeeld in het topic waar we lijsten introduceren. De code zit hier weggestopt in de module profiling die we eerder importeerden. Daarin hebben we gelijkaardige functies gereedgezet om power, fast-power, fib en vfib te plotten.

Grote $O$ Notatie¶

Jammer genoeg is profiling niet altijd de beste methode om op een wetenschappelijke manier over de uitvoeringssnelheid van een algoritme te spreken. Een ongelukkig profile kan ons immers een totaal verkeerd beeld geven van de uitvoeringssnelheid van het algoritme in het algemeen. De gemeten tijden kunnen immers afhangen van een hele reeks technische factoren die dikwijls afhangen van andere programma’s die op je computer draaien.

Zelfs indien de profile technisch redelijk goed is opgesteld kan het toch nog steeds zijn dat er bepaalde uitzonderlijke soorten invoer bestaan waarop het algoritme heel goed of heel slecht scoort. Voor fac, power en fib is het vrij triviaal om te begrijpen wat er voor iedere $n$ zal gebeuren maar voor de meeste algoritmen is dat lang niet het geval en zal procedure voor sommige invoerwaarden veel meer werk verrichten dan voor andere. Dat zal vanaf volgende topic reeds het geval zijn. Je zal dan maar net toevallig een profile maken met die slecht gekozen invoerwaarden.

Om hieraan te verhelpen bespreken we nu een wetenschappelijke methode om over de snelheid van algoritmen te spreken: de grote $O$ notatie. Het idee achter deze notatie is van -voor een gegeven algoritme $A$-

een functie $f_A(n)$ te bepalen die het aantal “uitvoeringsstapjes” van $A$ telt in functie van de grootte van de invoer, $n$.

We zullen de notatie toelichten aan de hand van een voorbeeld. Dat bestaat uit het schrijven van Python functies om natuurlijke getallen in decimale notatie te converteren naar binaire notatie, en omgekeerd.

Interludium: Binaire Getallen¶

Computers werken diep binnenin met twee verschillende voltages die door computerwetenschappers als “0” en “1” worden geïnterpreteerd. Dit zijn de beroemde bits (Eng.: binary digits). Massieve hoeveelheden schakelingen combineren zulke bits met mekaar en dit is eigenlijk in een notendop de werking van een computer. Alles maar dan ook alles wordt intern voorgesteld door lange reeksen nullen en enen. Zelfs Python programma’s worden uiteindelijk op deze manier voorgesteld.

Om dit toe te lichten zullen we nu bestuderen hoe we natuurlijke getallen kunnen voorstellen in deze binaire notatie. Neem bijvoorbeeld het getal $186$. Het bestaat uit $3$ tiendelige cijfers waarbij de positie bepaalt voor hoeveel ieder cijfer meetelt. Zo staat $6$ op de $0$de positie, staat $8$ op de eerste positie en staat $1$ op de $2$de positie. In feite geldt daarom dat $186 = 1 \times 10^2 + 8 \times 10^1 + 6 \times 10^0$. We kunnen het getal $186$ echter ook opschrijven in het binaire stelsel. In plaats van cijfers te gebruiken tussen $0$ en $9$ gebruiken we enkel de cijfers tussen $0$ en $1$. Ook nu bepaalt de positie van iedere $0$ of $1$ voor hoeveel ze meetelt. Dat ziet er voor ons voorbeeld als volgt uit: $186 = 1 \times 2^7 + 0 \times 2^6 + 1 \times 2^5 + 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0$ zodat $186$ in binaire notatie wordt geschreven als $10111010$.

Om van $186$ de decimale cijfers te bepalen delen we telkens door $10$. De rest bij deling geeft het cijfer en we vervolgen het proces met het resultaat van de deling. $186 \div 10$ geeft $6$ als rest (het $0$de cijfer) en we vervolgen met $18$. $18 \div 10$ geeft $8$ als rest (het $1$ste cijfer) en we vervolgen met $1$. $1 \div 10$ geeft $1$ als rest (het $2$ de cijfer) en het proces is afgelopen. Indien we nu delen door $2$ in plaats van door $10$ krijgen we op exact dezelfde manier de binaire voorstelling:

$186 \div 2 = 93$ (rest $0$).

$93 \div 2 = 46$ (rest $1$)

$46 \div 2 = 23$ (rest $0$)

$23 \div 2 = 11$ (rest $1$)

$11 \div 2 = 5$ (rest $1$)

$5 \div 2 = 2$ (rest $1$)

$2 \div 2 = 1$ (rest $0$)

$1 \div 2 = 0$ (rest $1$)

zodat $186 = 10111010$.

Hieronder zie je de Python uitwerking van een functie dec_to_bin_aux die een decimaal getal number omzet naar een binair getal. Dat binaire getal zal als een tupel met nullen en enen voorgesteld worden in Python.

def dec_to_bin_aux(number):
    if number==0:
        return ()
    elif number%2==1:
        return dec_to_bin_aux(number//2) + (1,)
    else:
        return dec_to_bin_aux(number//2) + (0,)

We bestuderen nu de werking van dec_to_bin_aux in detail. De functie is duidelijk recursief. De stopconditie bestaat uit het testen van number==0, in dat geval wordt een leeg tupel teruggegeven. De recursie gebeurt op basis van het afbouwen van number. Dat zien we duidelijk in iedere recursieve oproep: deze gebeuren telkens met number//2 (let op, wel met // d.w.z. de gehele deling). Merk op dat er twee recursieve aanroepen in de body staan maar dat dit toch geen voorbeeld is van boomrecursie. In tegenstelling tot bijvoorbeeld fib staan beide recursieve aanroepen in een verschillende tak van de if test zodat er eigenlijk maar één aanroep gebeurt in iedere stap van de recursie. In elke stap delen we number dus door $2$. Om het resultaat te vormen plakken twee tupels aan elkaar (c.f. de + operator): het tupel dat number//2 binair voorstelt aangevuld met het 1-tupel (1,) of met het 1-tupel (0,) afhankelijk of number even of oneven is. Dat wordt bepaald door de test number%2==1.

We hebben de functie “aux” genoemd (Eng.: auxiliary) omdat dit toch nog niet de uiteindelijke functie is om getallen naar hun binaire voorstelling om te vormen. Indien we bovenstaande functie oproepen met $0$ krijgen we gewoon het lege tupel terug en dat is niet de bedoeling: de binaire representatie van $0$ is het 1-tupel (0,). Dat wordt opgelost in de finale versie dec_to_bin die bovenstaande functie als hulpfunctie gebruikt (vandaar “aux”):

def dec_to_bin(number):
    if (number==0):
        return (0,)
    else:
        return dec_to_bin_aux(number)

dec_to_bin(0)

(0,)

dec_to_bin(186)

(1, 0, 1, 1, 1, 0, 1, 0)

dec_to_bin(1)

(1,)

dec_to_bin(7)

(1, 1, 1)

dec_to_bin(8)

(1, 0, 0, 0)

Het omgekeerde is al even eenvoudig. We schrijven een procedure bin_to_dec die een binair getal in de vorm van een tupel met nullen en enen als argument krijgt, en het corresponderende decimale getal teruggeeft. We gaan opnieuw recursief te werk. Beschouw bijvoorbeeld het binaire getal $110$. Dat is $1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0$. Dat kunnen we schrijven als $2 \times (1 \times 2^1 + 1 \times 2^0) + 0$ wat $11$ binair maal $2$ plus $0$ is. Analoog is bijvoorbeeld $111$ te schrijven als $2 \times (1 \times 2^1 + 1 \times 2^0) + 1$ wat dus $11$ binair maal $2$ is plus $1$. We moeten dus telkens het laatste binaire cijfer tellen bij het dubbele van de andere binaire cijfers omgezet naar decimaal. Hoe dikwijls dient dat te gebeuren? Uiteraard voor elk binair cijfer dat we hebben en dat is precies de lengte van het tupel.

In Python ziet dat er als volgt uit: bin_to_dec krijgt een tupel binary als argument en roept meteen to_dec_aux op met twee argumenten: datzelfde tupel en de lengte van dat tupel. Het is op dit tweede argument dat de recursieve aanroepen zullen gebaseerd zijn: het getal n zal aftellen van de lengte tot $0$ en dit getal gebruiken we om in elke stap van de recursie het tupel te indexeren om het $n'de$ binaire cijfer uit te lezen.

def to_dec_aux(tup,n):
    if n==0:
        return tup[0]
    elif tup[n] == 0:
        return  2 * to_dec_aux(tup,n-1) 
    else:
        return (2 * to_dec_aux(tup,n-1))+1
        
def bin_to_dec(binary):
    return to_dec_aux(binary,len(binary)-1)

bin_to_dec(( 0,))

bin_to_dec(( 1, 1, 0))

bin_to_dec(( 1, 0, 0, 1))

Stappen in de Grote O Notatie¶

Laat ons nu proberen van te bepalen welk soort proces (lineair, logaritmisch, exponentieel,…) bin_to_dec en dec_to_bin opleveren zonder te profilen. Dit kunnen we doen door het aantal computationele stappen te tellen die dec_to_bin zal uitvoeren om een binair getal te maken.

Wat bedoelen we precies met “computationele stappen”? Iedere basisactie van de Python evaluator zullen we als computationele stap beschouwen: een optelling, een vermenigvuldiging, een toekenning (t.t.z het uitvoeren van =), een vergelijkingstest (t.t.z het uitvoeren van ==), enzoverder. Ook het oproepen van een functie zullen we als computationele stap beschouwen. Hiermee bedoelen we de stap die de evaluator moet maken om van de oproeper over te gaan naar de eerste regel van de body van de opgeroepene. De body zelf zal meestal uit meerdere computationele stappen bestaan. Ook de terugkeer d.m.v. return correspondeert met één computationele stap: het doet de evaluator van de opgeroepene terugspringen naar de plaats in de oproeper. Al deze stapjes vragen tijd en het is daarom dus onze bedoeling om ze precies te gaan tellen.

Analyse van `dec_to_bin`¶

Bij oproep van dec_to_bin met een decimaal getal number onderscheiden we $2$ gevallen.

Stel dat number gelijk is aan $0$. De test number==0 zal dus waar zal zijn. Bijgevolg zal Python het 1-tupel (0,) maken en met return teruggeven. In totaal $3$ stappen dus.
Indien de test echter vals is, zal to_bin_aux worden opgeroepen. Dat levert in totaal $3$ stappen (één voor de test, één voor de oproep en één voor de return), plus uiteraard het aantal stappen dat nodig is om to_bin_aux uit te voeren:

We bekijken daarom ook to_bin_aux in detail. De body van deze recursieve functie zal telkens testen of number==0.

Indien de test waar is, wordt het lege tupel weergegeven en is de functie klaar. Dat zijn 2 stappen inclusief de test.
Indien de test vals is, wordt number%2==1 getest (2 stappen) en wordt afhankelijk van de waarheid (0,) of (1,) geplakt aan het resultaat van de recursieve oproep met number/2. In totaal zijn dat 5 stappen (1 om number/2 te berekenen, 1 om de recursieve oproep te doen, 1 om het 1-tupel te maken, 1 om de + te doen en nog 1 om met de return terug te keren). De eerste test, de tweede test en de recursieve oproep nemen in totaal dus $1+2+5$ stappen in beslag. Deze $8$ stappen gebeuren echter in elke recursieve oproep. Enkel de allerlaatste keer is de eerste test waar waarbij slechts $2$ stappen nog nodig zijn.

In totaal krijgen we dus $8r+2$ stappen waarbij $r$ het aantal recursieve oproepen is. $r$ is precies het aantal keren dat we number door $2$ kunnen delen alvorens we bij nul uitkomen. We zoeken dus $r$ zodat $\frac{\texttt{number}}{2^r} = 0$ en dat is per definitie natuurlijk $\lceil log_2(\texttt{number}) \rceil$.

Deze analyse laat ons dus toe te zeggen dat dec_to_bin, toegepast op een getal $n$, in totaal

\[\begin{split}\left\{ \begin{array}{ll} 3~\textrm{stappen neemt} & \textrm{als}~ n=0 \\ 8\lceil log_2(n) \rceil +5~\textrm{stappen neemt} & \textrm{als}~ n > 0 \end{array}\right.\end{split}\]

Merk op dat deze analyse helemaal onafhankelijk is van technologische factoren zoals het type van computer of het bouwjaar (en dus snelheid) ervan. Het levert ons een exacte beschrijving op van het aantal computationele stapjes die dec_to_bin nodig heeft om een decimaal getal om te vormen naar zijn binaire representatie. Net zoals fast_power genereert dec_to_bin dus een logaritmisch proces. We zijn hier echter op een totaal andere manier achter gekomen.

Analyse van `bin_to_dec`¶

Laat ons nu de omgekeerde functie bin_to_dec bestuderen. Een oproep ervan resulteert in exact $4$ computationele stappen: de oproep van len, de oproep van -, de oproep van to_dec_aux en de return. Indien we het aantal computationele stappen nu gaan tellen voor to_dec_aux zien we algauw dat het antwoord afhangt van de waarden in het tupel waarmee je de functie oproept.

Uiteraard hangt het aantal stappen af van de lengte van dat tupel. Het is duidelijk dat een lang tupel veel meer werk zal vragen dan een kort tupel. Maar zelfs bij tupels van gelijke lengte hangt het aantal stappen ook af van de cijfers (t.t.z. $0$ of $1$) die in dat tupel zitten. Als we bvb. to_dec_aux oproepen met een tupel dat allemaal nullen bevat dan zal de tweede test telkens opnieuw waar zijn en zal telkens de tweede tak van de if-test gekozen worden. Als we daarentegen to_dec_aux oproepen met een tupel dat allemaal enen bevat dan zal iedere recursieve oproep in de derde tak van de if-test belanden. In beide takken wordt to_dec_aux recursief aangeroepen. Beide aanroepen verschillen in het feit dat de derde tak ná de recursieve oproep nog $1$ bij het resultaat optelt alvorens uit de functie terug te keren. De derde tak vereist dus 1 computationele stap meer dan de tweede.

Worst-case vs. Best-case Analyse¶

Dit leidt ons tot twee totaal verschillende manieren om naar het aantal computationele stappen te kijken dat de uitvoering van een functie vereist. In een worst-case analyse tellen we het aantal computationele stappen voor een invoer die een maximale hoeveelheid werk vereist. In een best-case analyse tellen we het aantal computationele stappen voor een invoer die een minimale hoeveelheid werk vereist. In ons voorbeeld doen we een worst-case analyse door het geval te beschouwen waarbij de functie wordt opgeroepen met een tupel dat enkel enen bevat. In dat geval zal steeds de derde tak van de if test gekozen worden (en we weten dat deze oproep 1 stapje meer vraagt dan de andere tak). De best-case analyse verkrijgen we door het geval te beschouwen waarbij de functie wordt opgeroepen met een tupel enkel bestaand uit nullen. In dat geval zal telkens de tweede tak van de if-test gekozen worden; d.i. de tak die het minste aantal computationele stappen genereert.

In de worst-case analyse roepen we de procedure bin_to_dec dus op met een tupel van enen. Meteen wordt len(binary)-1 bepaald en wordt to_dec_aux opgeroepen en het resultaat hiervan teruggegeven met return. In totaal $4$ stappen dus. Dan gaat de recursie zijn werk doen, in totaal $n$ keer als $n$ de lengte van het tupel is. Telkens wordt n==0 bepaald (wat vals is), wordt tup[n]==0 getest. Aangezien dat False oplevert, gaan we de else-tak in. Daar wordt n-1 bepaald, wordt de functie recursief opgeroepen en wordt er teruggekeerd met return na de waarde te hebben vermenigvuldigd met $2$ en er $1$ te hebben bij opgeteld. In totaal dus $8$ stappen. Dat geeft ons dus $8n$ stappen voor de recursie. De allerlaatste keer wordt de test n==0 succesvol uitgevoerd en wordt de return uitgevoerd met tup[0]. Dat zijn 3 stappen. Alles tesamen geeft dat dus $4+3+8n = 8n+7$ computationele stappen.

De best-case analyse gebeurt volledig analoog. Het enige verschil is dat nu telkens de tweede tak van de if-test gekozen wordt. Telling van het aantal stappen geeft $7$ stappen in iedere recursieve aanroep (omdat er na vermenigvuldiging met $2$ géén $1$ bij opgeteld wordt). Dat geeft in totaal dus $7n+7$ stappen.

Voor sommige algoritmen heeft het ook zin om een average-case analyse uit te voeren. Hierbij gaat men kijken hoeveel stappen een algoritme gemiddeld uitvoert. Aangezien men hiervoor eigenlijk een goed zicht op de stochastische verdeling van de mogelijke invoer nodig heeft, is een average-case analyse doorgaans zeer ingewikkeld. Het resultaat is bovendien dikwijls gelijk aan de worst-case analyse.

Van aantal stappen naar Grote $O$ Notatie¶

We kunnen ons op dit ogenblik de vraag stellen of het wel de moeite loont om zulks een gedetailleerde analyse te maken van onze algoritmes. Inderdaad, het maakt niet echt uit of een algoritme $10n$ dan wel $8n$ stappen vereist. De duur van iedere stap is immers verschillend (bijvoorbeeld is in de meeste computers de vermenigvuldiging trager dan de optelling) en hangt bovendien van zeer veel technische factoren af (bvb. van je operating system, van de versie van Python, enzoverder). Een algoritme dat $13n$ stappen doet kan dus toch nog sneller zijn dan een ander algoritme dat slechts $9n$ stappen doet. Wat wel belangrijk is, is de grootte-orde van $n$. Een algoritme dat $5n$ stappen doet kan wel voor kleine $n$ weliswaar trager zijn dan een algoritme dat $n^2$ stappen doet, maar eens we de invoer groter maken dan een zekere $n_0$ zal het algoritme dat $n^2$ stappen doet veel trager zijn dan een algoritme dat $5n$ stappen doet en gelijk welk ander algoritme dat $a.n+b$ stappen doet.

Indien ons algoritme een lineair aantal stappen vereist, doen $a$ en $b$ er dus niet toe. Dit zullen we noteren als $O(n)$. Als we dus zeggen dat “een algoritme in $O(n)$ is” dan bedoelen we dat het algoritme een lineair aantal stappen vereist. Analoog hiermee kunnen we zeggen dat in de analyse van dec_to_bin die resulteerde in $8.\lceil log_2(n) \rceil+5$ (waarbij $n$ het getal is dat geconverteerd dient te worden) de $8$, de $2$ en de $5$ er eigenlijk niet toe doen. dec_to_bin is een logaritmisch process en dat zullen we voortaan noteren als $O(log(n))$.

In ons dec_to_bin voorbeeld is zowel de best-case analyse als de worst-case analyse in $O(log(n))$. Ook voor bin_to_dec zijn zowel de best-case als de worst-case analyse in $O(n)$. Dit is echter zelden het geval. In een later topic rond zoek- en sorteeralgoritmen zullen we bijvoorbeeld een algoritme zien dat in $O(n)$ is in de best-case maar dat in $O(n^2)$ is voor de worst-case, alsook een algoritme dat in $O(n.log(n))$ is in de best-case maar in $O(n^2)$ in de worst-case.

Wiskundig gezien correspondeert $O(n)$ met de verzameling van alle functies die niet sneller stijgen dan een rechte. M.a.w., $O(n)$ is de verzameling van alle functies die van boven te begrenzen zijn m.b.v. een veelvoud van de eerste bissectrice (vanaf een bepaalde beginwaarde $n_0$). Analoog is $O(n^2)$ de verzameling van alle functies die van boven begrensd kunnen worden door een parabool. In het algemeen: $$O(g(n)) = \{ f | \exists c, n_{0} \geq 0 : \forall n \geq n_{0} : 0 \leq f(n) \leq c g(n) \}$O(g(n))$ is dus de verzameling van alle functies $f$ die van boven te begrenzen zijn door een veelvoud van $g$ (vanaf een zekere $n_0$; dus voldoende groot).

$O$ wordt gebruikt om functies in families onder te verdelen zodat constanten geen rol spelen. Zo zijn $5n$, $\frac{n}{34}$ en $6n+88$ allen in $O(n)$ en zijn $5n^2$, $n^2+5n+8$ maar ook $5n$ allen in $O(n^2)$. $5n^2$ is echter niet in $O(n)$ want we kunnen een parabool nooit door een rechte van boven begrenzen: hoe groot we de constante ook kiezen, de parabool zal altijd boven de rechte uitsteken vanaf een bepaalde waarde. We laten de theoretische studie van $O$ over aan de wiskunde cursussen.

De groepen van functies waar men in de computerwetenschappen het meeste gebruik van maakt zijn opgelijst in onderstaande tabel. Vergelijk bijvoorbeeld maar eens het aantal stappen dat een logaritmisch (t.t.z. een $O(log(n))$) algoritme, een lineair (t.t.z. een $O(n)$) algoritme en een exponentieel (t.t.z. $O(2^n)$) algoritme uitvoeren voor $n=1024$.

$n$	$log(n)$	$\sqrt n$	$n$	$n.log(n)$	$n^{2}$	$n^{3}$	$2^{n}$
2	1	2	2	2	4	8	4
4	2	2	4	8	16	64	16
8	3	3	8	24	64	512	256
16	4	4	16	64	256	4096	65536
32	5	6	32	160	1024	32768	4294967296
64	6	8	64	384	4096	262144	$1.85 \times 10^{19}$
128	7	12	128	896	16384	2097152	$3.40 \times10^{38}$
256	8	16	256	2048	65536	16777216	$1.16 \times10^{77}$
512	9	23	512	4608	262144	134217728	$1.34 \times 10^{154}$
1024	10	32	1024	10240	1048576	1073741824	$1.79 \times 10^{308}$
…………..	…………..	…………..	…………..	………………	………………	………………….	……………………..

Samenvatting¶

In dit onderdeel van de cursus hebben we het fenomeen recursie bestudeerd. Recursie is een zeer krachtig concept aangezien het toelaat om vrij ingewikkelde processen op een zeer korte en zeer elegante wijze neer te schrijven in Python. Recursie is dan ook één van de krachtigste wapens in de computerwetenschappen. Recursie geeft ons immers de mogelijkheid om complexiteit te beheersen, en dat is in gelijk welke wetenschap een goede eigenschap. Natuurlijk is recursie niet beperkt tot Python. Elke moderne programmeertaal ondersteunt recursie en moedigt het gebruik ervan aan.

Recursieve functies geven aanleiding tot computationele processen waarvan de looptijd relevant is. Indien we het aantal recursieve aanroepen van zo’n functie gaan meten (hetzij door tracing, hetzij door profiling, hetzij door de grote $O$ notatie te gebruiken), dan kunnen we spreken van verschillende soorten processen. Tot nu toe hebben we o.m. te maken gehad met lineaire, logaritmische en exponentiële computationele processen. Met de grote $O$ notatie zeggen we dat dit computationele processen zijn die respectievelijk in $O(n)$, $O(log(n))$ en $O(2^n)$ zijn.

De recursieve functies die we hebben laten zien hebben werkten in eerste instantie op getallen. In het volgende topics onderzoeken we nog hoe we recursieve functies kunnen bouwen die lijsten van waarden gebruiken of die werken op willekeurige recursieve gegevens (i.h.b. geneste tupels en geneste lijsten).

Inleiding tot de Computerwetenschappen

TOPIC 4: Recursieve Functies¶

Recursie en Recursieve Processen¶

Procesvisualisatie: Tracing¶

Procesvisualisatie: Profiling¶

Soorten Computationele Processen¶

Logaritmische Processen¶

Exponentiële Processen¶

Traces en Profiles maken in Python¶

Tracing¶

Profiling¶

Grote \(O\) Notatie¶

Interludium: Binaire Getallen¶

Stappen in de Grote O Notatie¶

Analyse van `dec_to_bin`¶

Analyse van `bin_to_dec`¶

Worst-case vs. Best-case Analyse¶

Van aantal stappen naar Grote \(O\) Notatie¶

Samenvatting¶

Inleiding tot de Computerwetenschappen

TOPIC 4: Recursieve Functies¶

Recursie en Recursieve Processen¶

Procesvisualisatie: Tracing¶

Procesvisualisatie: Profiling¶

Soorten Computationele Processen¶

Logaritmische Processen¶

Exponentiële Processen¶

Traces en Profiles maken in Python¶

Tracing¶

Profiling¶

Grote \(O\) Notatie¶

Interludium: Binaire Getallen¶

Stappen in de Grote O Notatie¶

Analyse van dec_to_bin¶

Analyse van bin_to_dec¶

Worst-case vs. Best-case Analyse¶

Van aantal stappen naar Grote \(O\) Notatie¶

Samenvatting¶

Analyse van `dec_to_bin`¶

Analyse van `bin_to_dec`¶